Tendremos Temas de:
Álgebra
geometría y estadística.
Estadística 21 01 2017
Actividad para estregar la próxima clase en hoja de bloc:
Descargar:
https://sorjuanaines.gnomio.com/mod/resource/view.php?id=301
Álgebra
15 11 16
Problemas de PG para practicar
álgebra
14 11 16
álgebra
10 11 16
Área de matemáticas
10 11 16
Resolver
los siguientes ejercicios:
1) Hallar el 39° término de una P.A. (-3, -5/4,..............).
2) Encontrar el término general dela P.A. (1,3,5,7,...........).
3) El 15° término de una P.A. es 20 y la razón es 2/7. Hallar el 1er término.
4) Calcular la razón de una P.A. (3,........., 8,.....) ;donde 8 es el 6to término.
5) Cuántos términos tienela
P.A. (4, 6,............., 30).
6) Determinar el 1er término dela P.A. en que el 15° término es
44 y la razón es 3.
7) El 5to término de una P.A. es 7 y el 7mo término es 25/3. Hallar la razón.
8) Hallar la suma de la progresión aritmética : (0,2; 0,7; 1,2;..................) ;siendo n = 12.
9) La suma de 3 números que están en P.A. es 21 y el producto de los mismos es 231. Calcular esos números.
10) Cuántos múltiplos de 5 existen entre el 18 y el 193.
11) Hallar la suma de los 72 primeros múltiplos de 11 que siguen a 76.
12) Interpolar 3 medios aritméticos entre -1 y 7.
13) Calcular 9no término dela P.G. (1/32, 1/16,
1/8,...................).
14) Determinar el término general (an) de la progresión geométrica :: (5, 25, 125,.............).
15) Hallar el número de términos de una P.G. (4, 8,................., 512).
16) La razón de una progresión geométrica es 1/2 y el 7mo término es 1/64. Hallar el 1er término.
17) La razón de una progresión geométrica de 5 términos es 4 y el último término es 1.280. ¿Cuál es el 1er término de dicha progresión?
18) En una P.G. de razón - 5 el 1er término es 25 y el último es -3.125. Determinar el número de términos de está progresión.
19) Calcular la suma de los términos de la progresión geométrica :: (3, 6,............,2.187).
20) Hallar la suma de los 7 primeros términos de una P.G. (-1/10, 1/5, -2/5,..............).
21) Interpolar 3 medios geométricos entre 1 y 81.
Resolver los
siguientes problemas:
1) Las sumas del 1er y 3er término de una progresión aritmética es
12; y las sumas del 2do y 5to término es 21. Hallar los términos y la
razón.
2) El 3er y 5to término de una P.A. suman 46; y el 4to y 6to término suman 58. Hallar la razón y el valor de dichos términos.
3) El 2do y 4to término de una P.A. suman 22; y el 3er y 6to término suman 34. Hallar el valor de las incógnitas.
4) El 4to y 3er término de una P.A. suman 2; y el 3er con el 5to término suman 4. Hallar las incógnitas.
5) La suma del 2do y 3er término de una progresión aritmética es -5 y la suma del 5to y 6to término es 13. Hallar la razón y el valor de dichos términos.
6) Las ganancias de 3 años de una empresa están en progresión aritmética. El 1er año ganó 10.000 $ y el 3er año 24.000 $. Cuál fue la ganancia del 2do año.
7) En el 1er mes de negocios una persona ganó 500 $ y en el último ganó 1.900 $. Sí en cada mes ganó 200 $ más que el mes anterior. ¿Cuántos meses tuvo el negocio?.
8) Se compra 1 artículo a pagar en 15 meses de este modo: 1 $ el 1er mes; 3 $ el 2do mes; 9 $ el 3er mes y así sucesivamente. Cuál es el importe del artículo.
9) Un hombre avanza en el 1er segundo de su carrera 6 mts. y en cada segundo posterior avanza25 cm . más que el anterior.
Cuánto avanzó en el 8vo segundo y qué
distancia habrá recorrido en ese tiempo.
10) Hallar las longitudes de los lados de un triángulo, sabiendo que están en progresión aritmética de razón igual a6 cm . y que su perímetro es igual a 54 cm .
11) En una progresión geométrica de razón positiva, la suma del 3er término con el 4to es 240 y la suma del 5to con el 6to es 3.840. Calcular la razón y formar la progresión.
12) Calcular la razón de una P.G. de 5 términos; sabiendo que la suma de los dos primeros términos es 120 y la suma de los dos últimos es 960.

estadística
Resumen de clase Moda y mediana para datos agrupados, descargar:
07 11 16
taller de estrategias de apoyo IV periodo
descargar y resolver para poder presentar la evaluación en la semana 9
06 11 16
álgebra
30 10 16
Enlaces para autoevaluarte en P.A
geometría
29 10 16
Enlaces para repasar volumen y áreas de prismas conos y pirámides
geometría
02 10 16
29 09 16
Tarea: empleando los moldes construir los poliedros siguientes:
álgebra
28 19 16
Enlaces con vídeos de ayuda para repasar progresiones aritméticas:
Juegos para practicar tus competencias y preparar las pruebas saber:
19 09 16
geometría
12 09 16
álgebra progresiones aritméticas, resumen de clase:
Progresiones aritméticas .Resumen de clase
Término general de una progresión aritmética
Interpolación de términos en una progresión aritmética
 d= (b-a)/m+1
d= (b-a)/m+1
Suma de términos equidistantes de una progresión aritmética
 a1,a2,a3,…..an-2.
an-2, an-3,an
a1,a2,a3,…..an-2.
an-2, an-3,an
Suma de n términos consecutivos de una progresión aritmética
 Sn= (a1+an).n/2
Sn= (a1+an).n/2 S5=(8-12).5/2
S5=(8-12).5/2
2) Escribir tres medios aritméticos entre 3 y 23.
3) Interpolar tres medios aritméticos entre 8 y -12.
4) El primer término de una progresión aritmética es -1, y el décimoquinto es 27. Hallar la diferencia y la suma de los quince primeros términos.
5) Hallar la suma de los quince primeros múltiplos de 5.
6) Hallar la suma de los quince primeros números acabados en 5.
7) Hallar la suma de los quince primeros números pares mayores que 5.
8) Hallar los ángulos de un cuadrilátero convexo, sabiendo que están en progresión aritmética, siendo d= 25º.
9) El cateto menor de un triángulo rectángulo mide8 cm .
Calcula los otros dos, sabiendo que los lados del triángulo forman una
progresión aritmética.
Notas del III periodo definitivas
Matemáticas:
Notas del III periodo luego de las estrategias de apoyo. Hacer clic para descargar o ver:
álgebra 31 08 16
Vídeos de ayuda para repasar problemas con ecuaciones cuadráticas.
Ecuaciones cuadráticas │pura, mixta, completa
Ecuaciones cuadráticas mixtas (parte 1)
Ecuaciones Cuadráticas por completación de
cuadrados - Ejercicio 2
Ecuaciones cuadráticas mixtas│compilado 2
discriminante ecuacion cuadratica
problema raices ecuacion cuadratica 101
problema ecuacion cuadratica 201
problema raices ecuacion cuadratica 201
planteo ecuacion cuadratica 101
álgebra 24 08 16
para repasar:
Resumen de clase
álgebra enlace para descargar la estrategia de apoyo del III periodo:
Autoevaluación del III periodo
estadística 14 08 16
Enlace para presentar el quiz de estadística pictogramas:
álgebra 10 08 16
Talleres de ecuaciones cuadráticas
Resolver por factorización:
geometría 06 08 16
Enlace para el quiz de geometría
álgebra 06 08 16
Realizar el siguiente taller en el cuaderno para ser sustentado.
estadística 17 07 16
Enlace para presentar el quiz virtual de estadística:
estadística 16 07 16
álgebra
12 06 16
Taller de problemas de ecuaciones 2x2, para practicar.
Enlaces para repasar sistemas de ecuaciones 2x2:
álgebra aprendamos mientras descansamos:
Las simetrías del universo | Documental Redes
Eduard Punset
El número de Oro - El Sello de Dios.
Donald en la tierra mágica de la matemática
APLICACIÓN DE LOS NÚMEROS EN LA VIDA DIARIA
geometría:
Enlaces para repasar elementos del círculo y circunferencia:
Área de un trapecio circular o cuadrilátero
curvilíneo
Perímetro y área de un sector de corona
circular
Longitud de un arco dentro de una
circunferencia
Área circunferencia y sector circular: Cabra
fuera redil.
Enlace para descargar la estrategia de apoyo del II periodo:
geometría 19 05 16
Repaso de ángulos de la circunferencia:
07 05 16 Álgebra
Aplicaciones de la función lineal:
Álgebra 28 04 16
Enlace para presentar el quiz virtual del Teorema de Pitágoras:
23 04 2016
Geometría
Realizar en el cuaderno las siguientes aplicaciones del teorema de Pitágoras:
22 04 2016
Resumen de relaciones y funciones:
17 04 2016
Enlace para descargar el libro" el hombre que calculaba"
https://www.thatquiz.org/es/classtest?VWZF9EG1
Enlaces para el quiz de geometría , presentar hasta el miercoles
16 04 2016
Enlace para el quiz virtual de Estadística:
28 02 2015
Enlaces para el quiz diagnóstico de finanzas personales:
9.1:
23 02 15
Presentación y socialización del blog de finanzas para el cambio adscrito al proyecto institucional,cátedra de emprendimiento:
https://finansor.wordpress.com/
22 02 2015
21 02 20
Página para practicar jugando.
Me la juego por saber:
El código Dane de Sorjuana es:
15 02 2015
Progresiones Aritméticas. Definición y Elementos:
El prisma. Definición, partes, tipos, área, volumen y ejemplos prácticos. Cálculo de áreas y volumen de prismas
Volumen de un prisma. Ejercicio práctico.
Septiembre 22 de 2014
Resumen de clase Progresiones aritméticas
Septiembre 20 de 2014
Enlaces para el quiz de geometría:
9.1:
Ecuaciones Logarítmicas Solución de una ecuación que contiene logaritmos Ecuación que contiene logaritmos Ecuación con logaritmos de bases distintas Ecuación con logaritmos de diferentes bases
Otros enlaces de interés:
Ecuaciones logarítmicas(Ejercicios)
Solución de ecuaciones logarítmicas
Agosto 27 de 2014
Actividad de apoyo para Álgebra.
Practicar ecuaciones en los siguientes enlaces, antes de presentar el quiz de apoyo.
Realizar los problemas antes de presentar el Quiz
1.Escribir una ecuación de segundo grado cuyas soluciones son: 3 y −2.
2.Factorizar:
3.Determinar k de modo que las dos raíces de la ecuación x2 − kx + 36 = 0 sean iguales.
4.La suma de dos números es 5 y su producto es −84. Halla dichos números.
5.Dentro de 11 años la edad de Pedro será la mitad del cuadrado de la edad que tenía hace 13 años. Calcula la edad de Pedro.
6.Para vallar una finca rectangular de 750 m² se han utilizado 110 m de cerca. Calcula las dimensiones de la finca.
7.Los tres lados de un triángulo rectángulo son proporcionales a los números 3, 4 y 5. Halla la longitud de cada lado sabiendo que el área del triángulo es 24 m².
8.Un jardín rectangular de 50 m de largo por 34 m de ancho está rodeado por un camino de arena uniforme. Halla la anchura de dicho camino si se sabe que su área es 540 m².
9.Calcula las dimensiones de un rectángulo cuya diagonal mide 75 m, sabiendo que es semejante a otro rectángulo cuyos lados miden 36 m y 48 m respectivamente.
10.Halla un número entero sabiendo que la suma con su inverso es 26/5
11.Dos números naturales se diferencian en dos unidades y la suma de sus cuadrados es 580. ¿Cuáles son esos números?
12.Dos caños A y B llenan juntos una piscina en dos horas, A lo hace por sí solo en tres horas menos que B. ¿Cuántas horas tarda a cada uno separadamente?
13.Los lados de un triángulo rectángulo tienen por medidas en centímetros tres números pares consecutivos. Halla los valores de dichos lados.
14.Una pieza rectangular es 4 cm más larga que ancha. Con ella se construye una caja de 840 cm3 cortando un cuadrado de 6 cm de lado en cada esquina y doblando los bordes. Halla las dimensiones de la caja.
15.Un caño tarda dos horas más que otro en llenar un depósito y abriendo los dos juntos se llena en 1 hora y 20 minutos. ¿Cuánto tiempo tardará en llenarlo cada uno por separado?
Taller de apoyo en geometría:
Para ambos novenos. Traer en hojas de block, resueltos los siguientes problemas:
Agosto 14 de 2014
Para noveno.
Presentar de álgebra los problemas de julio 26 de 2014
y de geometría los problemas de julio 15 de 2014 que aparecen es te blog,en hojas de block.
Agosto 13 de 2014
Quiz virtual de sistemas de ecuaciones lineales. Hasta 16 08 14
Para 9.2:
Quiz virtual de sistemas de ecuaciones lineales. Hasta 16 08 14
Para 9.1:
Agosto 12 de 2014
Problema resuelto con ecuaciones de segundo
grado Ejemplo 4
APLICACIÓN DE ECUACIONES CUADRÁTICAS caja de latón.
Otros enlaces de interés
Ecuaciones de Segundo Grado por Fórmula General Solución de una ecuación cuadrática por fórmula general Solución de una ecuación cuadrática por factorización y fórmula. Ecuaciones de 2º grado. Fórmula General
Julio 30 de 2014
Geometría
Trapecio circular:
Julio 26 de 2014
Método de igualación
Problemas de aplicación
Julio 23 de 2014
Geometría:
Julio 20 de 2014
Geometría
Julio 17 de 2014
Otros métodos de solución de ecuaciones simultáneas.
Por determinantes ( regla de cramer)
otro video Método por igualación Otro video.
Julio 15 de 2014
Problemas de geometría.
Realizarlos en el cuaderno.
Julio 07 de 2014
Solución de un sistema de ecuaciones 2x2 por el método de reducción o eliminación:
Otra Solución por reducción: Solucion de un sistema 2x2 por método gráfico
Mayo 31 de 2014
Hacer clic en :
Viernes 4 de Abril de 2014
Enlace para descargar resumen de relaciones y funciones:
Es es para ambos novenos, para practicar y autoevaluarse:
http://www.vitutor.com/fun/1/a_2_e.html
http://www.vitutor.com/fun/1/a_3_e.html
Viernes 15 de Febrero de 2014
Taller Resumen de geometría
Descargar el ducumento de Ángulos del siguiente enlace:
26 de Febrero de 2014
Estudiar Ángulos Entre Paralelas en el enlace:
http://www.aulafacil.com/matematicas-basicas/geometria/curso/Lecc-14.htm
http://www.youtube.com/watch?v=qTQXBYkekms
27 de febrero de 2014
Taller de Potencias y Raíces.
Descargar de:
https://www.dropbox.com/s/jwsiwy9skxmk1k6/Ejercicios%20de%20N%C3%BAmeros%20Reales%20potencias%20y%20raices.doc
04 de Marzo de 2014
Álgebra
geometría y estadística.
Álgebra 09 02 17
Álgebra 28 01 17
geometría
álgebra
Razones y proporciones
Enlace para descargar la teoría
Razones y proporciones ¿ qué
es una razón y una proporción ?
t de thales
División de un segmento en
partes iguales (teorema de Tales)
Teorema de Thales -
Ejercicio 1
Encontrar el lado de un
triángulo usando el teorema de Tales Geometría 385
Repasar
operaciones básicas en el campo de los números reales con aplicaciones
cotidianas.
1.
Un comerciante
compró una pieza de tela de 23 metros por $ 195.000 . Después vendió cada metro
a $ 18.750. ¿Cuánto gana el comerciante en la venta de cada metro?
2.
Adrían compró
una moto por un valor de $ 9.480.000. Primero pagó la mitad del
valor y el resto en 12 mensualidades iguales. ¿Cuánto pagó en cada mensualidad?
3. Alicia ha
vendido hoy 24 sillas iguales. Un armario y un sillón por un valor de
3.200.000. El armario costó $ 1.750.000 y el sillón $850.000. ¿Cuánto costó
cada silla?
4. Un
ciempiés tiene 42 patas. Este levanta 3/7 de sus patas. Cuántas patas
levanta?
5. En una
granja hay 150 animales. 2/6 son vacas, 1/5 son gallinas, 3/10 cerdos, el
resto son patos. ¿Cuantos animales de cada clase hay?
6. Un rollo de tela
mide 36.25 metros de largo y tiene 2.30 metros de ancho. ¿Cuántos tozos
cuadrados de 1.15 metros se pueden obtener de él?
7 En Diciembre
compré unos tenis de $ 85.000 con un descuento del 15%; una camiseta de $28.000
con un descuento del 10%; y unos pantalones de $62.000 con descuento del 20%.
Si llevaba $ 200.000. a) ¿Cuánto dinero me sobró? b) ¿ Cuánto fue el
descuento total? C) ¿Cuánto me ahorré en los tenis? D) ¿De cuánto habría
sido el importe sin los descuentos?
geometría 05 02 17
Leer el texto y responder la preguntas en hoja de bloc para la próxima clase
Leer el texto y responder la preguntas en hoja de bloc para la próxima clase
Los
pensadores griegos Heródoto y Aristóteles no quisieron arriesgarse a situar los
orígenes de la geometría en una época anterior a la de la civilización egipcia,
pero está claro que la geometría en la que ellos pensaban tenía sus raíces en
una antigüedad mucho mayor. Herodoto sostenía que la geometría se había
originado en Egipto porque creía que dicha materia había surgido allí a partir
de la necesidad practica de volver a trazar lo linderos de las tierras después
de la inundación anual del río del Nilo.
Aristóteles en cambio sostenía, que el cultivo y el desarrollo de la geometría
en Egipto se había visto impulsado por la existencia allí de una amplia clase
sacerdotal ociosa. Podemos considerar que los puntos de vista de Herodoto y Aristóteles
representan dos teorías opuestas acerca de los orígenes de la geometría, la
primera defendiendo un origen basado en una necesidad practica y la segunda un
origen basado en el ocio y el ritual sacerdotal. El hecho de que a los
geómetras egipcios se les llamara a veces,”los tensores de la cuerda”(o
agrimensores) se puede utilizar para apoyar cualquiera de las dos teorías,
porque las cuerdas se usaron tanto para bosquejar los planos de los templos
como para reconstruir las fronteras borradas entre los terrenos.
De
acuerdo al texto responder.
1. El propósito del autor en
el escrito es:
a. Sustentar la tesis de Aristóteles
sobre la aparición de la geometría.
b. Explicar como la clase
sacerdotal egipcia impulsó el desarrollo de la geometría.
c. Defender la posición de
Herodoto y Aristóteles sobre los orígenes de la geometría.
d. Exponer los diferentes
puntos de vista sobre los orígenes de la geometría.
2. De los siguientes
enunciados no se deduce del texto:
a. Las cuerdas fueron
empleadas por los egipcios para medir distancias
b. El ocio de los sacerdotes
egipcios obstaculizó el desarrollo de la geometría.
c. Los orígenes de la
geometría se deben buscar antes de la civilización egipcia.
d. El pueblo egipcio
contribuyó al desarrollo de la geometría en razón a desastres naturales.
3. El autor desarrolla su escrito
principalmente en:
a. Argumentaciones falsas.
b. Especulaciones de
pensadores griegos.
c. Ejemplificaciones de
sabios antiguos.
d. Puntos de vista supuestos
4. De acuerdo con el
contenido del fragmento, este se puede titular:
a. Herodoto y Aristóteles:
dos grandes del pensamiento griego.
b. Punto de vista Aristotélico
sobre la aparición de la geometría.
c. Los orígenes de la
geometría.
d. La geometría una ciencia
polémica.
5. La agrimensura que se
menciona en el texto hace referencia a:
a. El arte de medir la
tierra.
b. El cuidado de los suelos.
c. La reconstrucción de las
fronteras borradas.
6. Del texto podemos ver que
la geometría nace de:
a.
Un capricho
b. Una necesidad económica.
c. Una necesidad política.
d. Un encargo religioso.
- Antiguamente
se le llamaba “ los tensores de la cuerda “ a los
- Griegos
- Egipcios
- Filósofos antiguos
- Gobernantes de turno
- Según
el texto la palabra geometría de refiere a:
- La medida de la tierra.
- Un concepto filosófico
- Un interés político
- Un concepto económico
- El
pensador que sostenía que la geometría aparece por una necesidad práctica
era
- Aristóteles
- Herodoto.
- Un egipcio
- Un sacerdote
- Los geómetras antiguos utilizaban cuerdas
para:
- Encerrar terrenos
- Medir terrenos
- Detener inundaciones
- Hacer rituales religiosos
álgebra
Descargar el libro " El hombre que calculaba" del siguiente enlace:
Actividad para estregar la próxima clase en hoja de bloc:
Descargar:
https://sorjuanaines.gnomio.com/mod/resource/view.php?id=301
Álgebra
15 11 16
Problemas de PG para practicar
1. El 2º término de una progresión geométrica es 6, y el 5º
es 48. Escribir la progresión.
2.
El 1er término
de una progresión geométrica es 3, y el 8º es 384. Hallar la razón, y la suma y
el producto de los 8 primeros términos.
3.
Interpolar tres medios geométricos entre 3 y
48.
4.
Calcular la suma de los primeros 5 términos
de la progresión : 3, 6, 12, 24, 48, ...
5.
Calcular la suma de los términos de la
progresión geométrica decreciente ilimitada: 1,1/2,1/4,1/8,1/16....
6.
Calcular el producto de los primeros 5
términos de la progresión: 3, 6, 12, 24, 48, ...
7.
Juan ha comprado 20 libros, por el 1º ha
pagado 1€, por el 2º 2 €, por el 3º 4 €, por el 4º 8 € y aí sucesivamente.
Cuánto ha pagado por los libros.
8.
Uniendo los puntos medios de los lados de un
cuadrado de lado l, se obtiene otro, en el que volvemos a hacer la misma
operación, y así se continua indefinidamente. Calcular la suma de las áreas de
los infinitos cuadrados.
9.
Hallar la fracción generatriz de
0.28282828...
10.Encontrar
la fracción generatriz de 8.2333333...
11.A las 9 de la mañana, una persona cuenta a tres amigos un secreto.
Media hora después, cada uno de estos tres amigos cuenta el secreto a otras
tres personas. Media hora más tarde, cada uno de éstos cuenta el secreto a
otras tres personas y así sucesivamente. Calcular cuántas personas saben el
secreto a las 2 de la tarde suponiendo que cada persona sólo cuenta el secreto
a otras tres personas y a nadie más durante el día y que ninguno ha recibido la
información varias veces.
14 11 16
Enlaces para repasar Progresiones geométricas:
Ayudas en videos:
Progresiones Geométricas - Ejercicio 1
Progresiones Geométricas - Ejercicio 2
Progresiones Geométricas - Ejercicio 3
álgebra
10 11 16
Progresiones Geométricas. Resumen de clase
10 11 16
 |
Institución
Educativa Sor Juana Inés de
“Solidaridad y compromiso
Trascendiendo en
|
||
ESTRATEGIA DE
APOYO
|
|||
Área Matemáticas
|
Grado 9
|
Cuarto Periodo
|
|
SOLUCIÓN DEL TALLER 30%
SUSTENTACIÓN DEL TALLER 70%
Resolver en hojas de block
Resolver
los siguientes ejercicios:
1) Hallar el 39° término de una P.A. (-3, -5/4,..............).2) Encontrar el término general de
3) El 15° término de una P.A. es 20 y la razón es 2/7. Hallar el 1er término.
4) Calcular la razón de una P.A. (3,........., 8,.....) ;donde 8 es el 6to término.
5) Cuántos términos tiene
6) Determinar el 1er término de
7) El 5to término de una P.A. es 7 y el 7mo término es 25/3. Hallar la razón.
8) Hallar la suma de la progresión aritmética : (0,2; 0,7; 1,2;..................) ;siendo n = 12.
9) La suma de 3 números que están en P.A. es 21 y el producto de los mismos es 231. Calcular esos números.
10) Cuántos múltiplos de 5 existen entre el 18 y el 193.
11) Hallar la suma de los 72 primeros múltiplos de 11 que siguen a 76.
12) Interpolar 3 medios aritméticos entre -1 y 7.
13) Calcular 9no término de
14) Determinar el término general (an) de la progresión geométrica :: (5, 25, 125,.............).
15) Hallar el número de términos de una P.G. (4, 8,................., 512).
16) La razón de una progresión geométrica es 1/2 y el 7mo término es 1/64. Hallar el 1er término.
17) La razón de una progresión geométrica de 5 términos es 4 y el último término es 1.280. ¿Cuál es el 1er término de dicha progresión?
18) En una P.G. de razón - 5 el 1er término es 25 y el último es -3.125. Determinar el número de términos de está progresión.
19) Calcular la suma de los términos de la progresión geométrica :: (3, 6,............,2.187).
20) Hallar la suma de los 7 primeros términos de una P.G. (-1/10, 1/5, -2/5,..............).
21) Interpolar 3 medios geométricos entre 1 y 81.
Resolver los
siguientes problemas:
1) Las sumas del 1er y 3er término de una progresión aritmética es
12; y las sumas del 2do y 5to término es 21. Hallar los términos y la
razón.2) El 3er y 5to término de una P.A. suman 46; y el 4to y 6to término suman 58. Hallar la razón y el valor de dichos términos.
3) El 2do y 4to término de una P.A. suman 22; y el 3er y 6to término suman 34. Hallar el valor de las incógnitas.
4) El 4to y 3er término de una P.A. suman 2; y el 3er con el 5to término suman 4. Hallar las incógnitas.
5) La suma del 2do y 3er término de una progresión aritmética es -5 y la suma del 5to y 6to término es 13. Hallar la razón y el valor de dichos términos.
6) Las ganancias de 3 años de una empresa están en progresión aritmética. El 1er año ganó 10.000 $ y el 3er año 24.000 $. Cuál fue la ganancia del 2do año.
7) En el 1er mes de negocios una persona ganó 500 $ y en el último ganó 1.900 $. Sí en cada mes ganó 200 $ más que el mes anterior. ¿Cuántos meses tuvo el negocio?.
8) Se compra 1 artículo a pagar en 15 meses de este modo: 1 $ el 1er mes; 3 $ el 2do mes; 9 $ el 3er mes y así sucesivamente. Cuál es el importe del artículo.
9) Un hombre avanza en el 1er segundo de su carrera 6 mts. y en cada segundo posterior avanza
10) Hallar las longitudes de los lados de un triángulo, sabiendo que están en progresión aritmética de razón igual a
11) En una progresión geométrica de razón positiva, la suma del 3er término con el 4to es 240 y la suma del 5to con el 6to es 3.840. Calcular la razón y formar la progresión.
12) Calcular la razón de una P.G. de 5 términos; sabiendo que la suma de los dos primeros términos es 120 y la suma de los dos últimos es 960.
TALLER
GEOMETRÍA 9º
Calcular el
volumen y el área total de:
1. Una esfera de Radio R= 10 cm .
2. Un cubo de 4 cm de arista
3. Un prisma rectangular con dimensiones l= 3cm , w= 4 cm , h= 5 cm .
4. Una pirámide de base cuadrada de 8 cm de lado y 24 cm de altura.
5. Un cilindro de altura h= 20 cm y
radio de la base R= 4cm
6. La apotema de la base de una pirámide
cuadrangular regular mide 12
cm y la altura de
la pirámide mide 16 cm .
Calcular el área total de la pirámide.
7. La altura de la base de una
pirámide triangular regular mide 9 cm y la apotema de la pirámide mide 18 cm . Calcular el área de
la pirámide.
8. El área total de una pirámide triangular
regular es de 600 cm2 y el lado de la base mide 12 cm . Calcular la altura de la pirámide.
9. Calcular el peso de 250 metros de alambre de
hierro. de 3 mm de diámetro. ( densidad del Fe = 7,8)
10. Calcular el volumen de una moneda de 20 mm de diámetro y 5 mm de espesor.
11. El ortoedro mostrado tiene a= 6cm , b=
8 cm y c= 10 cm . Calcula la diagonal principal D.
12. El
ortoedro mostrado tiene dimensiones l= 4 cm , w= 3cm, h= 6cm.
Calcular:
1. Área de la base
2. Área lateral
3. Área total
4. Volumen
5. Área del rectángulo rayado
Estrategia de apoyo 9º estadística
La tabla de frecuencias siguiente
corresponde a la natalidad en una determinada ciudad.
Clase
|
Intervalo
|
Marca de
clase: Xi
|
Frecuencia absoluta:
fi
|
Frecuencia
absoluta acumulada: Fi
|
Frecuencia porcentual acumulada
%
|
Xi.fi
|
|
1º
|
44-51
|
47,5
|
16
|
16
|
10,67
|
10,67
|
760
|
2º
|
51-58
|
54,5
|
19
|
35
|
12,67
|
23,33
|
1035,5
|
3º
|
58-65
|
61,5
|
24
|
59
|
16
|
39,33
|
1476
|
4º
|
65-72
|
68,5
|
31
|
90
|
20,67
|
60
|
2123,5
|
5º
|
72-79
|
75,5
|
23
|
113
|
15,33
|
75,33
|
1736,5
|
6º
|
79-86
|
82,5
|
15
|
128
|
10
|
85,33
|
1237,5
|
7º
|
86-93
|
89,5
|
13
|
141
|
8,67
|
94
|
1163,5
|
8º
|
93-100
|
96,5
|
9
|
150
|
6
|
100
|
|
150
|
10401
|
Hallar la moda, la mediana, la media o promedio aritmético y
realizar un gráfico de barras y trazar la ojiva y ubicar la moda y la mediana
en este gráfico.
Resumen de clase Moda y mediana para datos agrupados, descargar:
07 11 16
taller de estrategias de apoyo IV periodo
descargar y resolver para poder presentar la evaluación en la semana 9
álgebra
P.G. Resumen de clase abrir o descargar
Álgebra 30 10 16
Enlaces para autoevaluarte en P.A
P:A
practicas
P.A Y P.G
geometría
29 10 16
Enlaces para repasar volumen y áreas de prismas conos y pirámides
ÁREA Y VOLUMEN DE UN PRISMA
RECTO
Área y volumen de una
pirámide - Operacionexito.com
Calcular la generatriz, el
área y el volumen del cono
Apotema, área y volumen de
la pirámide cuadrangular
Área y volumen de una
pirámide - Operacionexito.com
ÁREA Y VOLUMEN DE UNA
PIRÁMIDE
Área de la pirámide
hexagonal regular
Volumen de la pirámide
hexagonal regular
02 10 16
taller de prismas, áreas y volúmenes
1. Los lados de la base de un pilar hexagonal regular miden 40 cm, y su altura 5 metros .Expresar en m2 el área de la superficie.
2. Uno de los ángulos de la base de un paralelepípedo recto mide 70°. ¿Cuánto miden los ángulos planos de todos sus diedros?
3. La diagonal de una de las caras de un cubo mide 4 cm . Calcular la diagonal principal del cubo
4. La diagonal principal de un cubo mide 6 cm. Calcular la diagonal de las caras.
5. Un cubo de 5 cm de arista es cortado por un plano inclinado que contiene las diagonales de las caras opuestas. Calcular el área de cada uno de estos cuerpos.
6. Un cubo de 5 cm de arista es cortado por un plano que pasa por sus 3 vértices de manera que la intersección sea un triángulo equilátero. Calcular el área de este triángulo.
7. Calcular el área total de un prisma de base hexagonal de lado 5 cm y altura 15 cm.
8. Calcular la arista de un cubo cuya área total es de 1 dm2.
9. Calcular la arista de un prisma triangular, si su altura es igual al lado de la base y el área total es de 1 dm2.
10. Una caja de leche tiene forma de prisma recto de base cuadrada de 8 cm de lado. Su diagonal principal mide 23 cm. Calcular los litros de leche que contiene.
11. Calcular el volumen de un prisma de base cuadrada de 8 cm de lado si su diagonal principal mide 23 cm
12. Calcular el volumen de un prisma recto que tiene por base un triángulo equilátero de 8 m de lado, y altura 14 m.
13. Calcular el área lateral de un prisma recto que tiene por base un triángulo equilátero de 8 m de lado, y altura 14 m.
14. Calcular el área total de un prisma recto que tiene por base un triángulo equilátero de 8 m de lado, y altura 14 m.
15. Un frasco de perfume tiene forma de prisma recto de base pentagonal regular de lado 6 cm y apotema 4 cm. Determinar cuántos ml de perfume puede contener.
16. Determinar el volumen de un prisma rectangular cuya base es un hexágono de lado 2 cm y altura 10 cm.
17. Determinar el área lateral de un prisma rectangular cuya base es un hexágono de lado 2 cm y altura 10 cm.
18. Determinar el área total de un prisma rectangular cuya base es un hexágono de lado 2 cm y altura 10 cm.
19. Calcular el volumen de un prisma recto de base hexagonal si su altura es 10 cm y su diagonal principal es la raíz cuadrada de 116 m.
20. Calcular el área total de un prisma recto de base hexagonal si su altura es 10 cm y su diagonal principal es la raíz cuadrada de 116 m.
geometría29 09 16
Tarea: empleando los moldes construir los poliedros siguientes:
Empleando los moldes construir los siguientes sólidos:
para practicar:
Pirámides ej
álgebra
28 19 16
Enlaces con vídeos de ayuda para repasar progresiones aritméticas:
Progresiones Aritméticas -
Ejercicio 1
Progresiones Aritméticas -
Ejercicio 2
Progresiones Aritméticas -
Ejercicio 3
Progresiones Aritméticas -
Ejercicio 4
Progresiones Aritméticas -
Ejercicio 5
Progresiones Aritméticas -
Ejercicio 6
problema progresion
aritmetica 101
problema progresiones
aritmeticas 201
La edad de 6 hermanos están
en progresión aritmética cuya suma es 106
problema progresiones
aritmeticas 201
Progresiones aritméticas
problema
https://www.youtube.com/watch?v=DSulSJbgzdw
Enlace para descargar el resumen de clase de P.A.
) Las sumas del 1er y 3er término de una progresión aritmética es 12; y las sumas del 2do y 5to término es 21. Hallar los términos y la razón.
2) El 3er y 5to término de una P.A. suman 46; y el 4to y 6to término suman 58. Hallar la razón y el valor de dichos términos.
3) El 2do y 4to término de una P.A. suman 22; y el 3er y 6to término suman 34. Hallar el valor de las incógnitas.
4) El 4to y 3er término de una P.A. suman 2; y el 3er con el 5to término suman 4. Hallar las incógnitas.
5) La suma del 2do y 3er término de una progresión aritmética es -5 y la suma del 5to y 6to término es 13. Hallar la razón y el valor de dichos términos.
6) Las ganancias de 3 años de una empresa están en progresión aritmética. El 1er año ganó 10.000 $ y el 3er año 24.000 $. Cuál fue la ganancia del 2do año.
7) En el 1er mes de negocios una persona ganó 500 $ y en el último ganó 1.900 $. Sí en cada mes ganó 200 $ más que el mes anterior. ¿Cuántos meses tuvo el negocio?.
8) Se compra 1 artículo a pagar en 15 meses de este modo: 1 $ el 1er mes; 3 $ el 2do mes; 9 $ el 3er mes y así sucesivamente. Cuál es el importe del artículo.
9) Un hombre avanza en el 1er segundo de su carrera 6 mts. y en cada segundo posterior avanza25 cm . más que el anterior.
Cuánto avanzó en el 8vo segundo y qué
distancia habrá recorrido en ese tiempo.
10) Hallar las longitudes de los lados de un triángulo, sabiendo que están en progresión aritmética de razón igual a6 cm . y que su perímetro es igual a 54 cm .
11) Una deuda debe ser pagada en 32 semanas; pagando 5 $ la 1ra semana, 8 $ la 2da semana, 11 $ la 3ra semana y así sucesivamente. Hallar el importe de la suma.
12) Los ahorros de los 3 primeros meses de una familia están en P.A. Sí en los 3 meses ha ahorrado 2.400 $ y el 1er mes ahorró la mitad de lo que ahorró el 2do mes. Cuánto ahorró cada mes.
13) El perímetro de un triángulo rectángulo es60 cm . Calcular las
longitudes de los lados, sabiendo que están en progresión aritmética.
14) Una piedra dejada caer libremente desde la azotea de un edificio recorre16,1 pies
en el 1er segundo y en cada segundo
posterior recorre 32,2
pies más que el 2do
anterior. Sí la piedra tarda 5 segundos en llegar al suelo. Cuál es la altura
del edificio.
15) Calcular las longitudes de los lados de un triángulo rectángulo, sabiendo que sus medidas expresadas en cm. son números que están en P.A. cuya razón es igual a 7.
16) Las ganancias mensuales de un comerciante durante 11 meses están en progresión aritmética. El 1er mes ganó 1.180 $ y el último 6.180 $. Cuánto más ganó en cada mes a contar del 2do mes, que en el anterior.
17) Determinar las longitudes de los lados de un triángulo rectángulo, sabiendo que están en P.A. de razón igual a 5.
18) Determinar el valor de "x" para que formen progresión aritmética de x ², (x + 2) ², (x + 3) ².
19) Determinar el valor de "x" para que formen P.A. de (3x - 1),
(x + 3), (x + 9).
Enlace para descargar el resumen de clase de P.A.
Nota:
Suma de términos equidistantes de una
progresión aritmética
Sean ai y aj dos
términos equidistantes de los extremos, se cumple que la suma de
términos equidistantes es igual a la suma de los extremos.
ai + aj = a1 +
an
a1,a2,a3,…….an-1,an-2,an
a3 +
an-2 = a2 +
an-1 = ... = a1 + an
8, 3, -2, -7, -12, ...
3 + (-7) = (-2) + (-2) = 8 + (-12)
-4 = -4 = -4
Problemas de progresiones Aritméticas para practicar) Las sumas del 1er y 3er término de una progresión aritmética es 12; y las sumas del 2do y 5to término es 21. Hallar los términos y la razón.
2) El 3er y 5to término de una P.A. suman 46; y el 4to y 6to término suman 58. Hallar la razón y el valor de dichos términos.
3) El 2do y 4to término de una P.A. suman 22; y el 3er y 6to término suman 34. Hallar el valor de las incógnitas.
4) El 4to y 3er término de una P.A. suman 2; y el 3er con el 5to término suman 4. Hallar las incógnitas.
5) La suma del 2do y 3er término de una progresión aritmética es -5 y la suma del 5to y 6to término es 13. Hallar la razón y el valor de dichos términos.
6) Las ganancias de 3 años de una empresa están en progresión aritmética. El 1er año ganó 10.000 $ y el 3er año 24.000 $. Cuál fue la ganancia del 2do año.
7) En el 1er mes de negocios una persona ganó 500 $ y en el último ganó 1.900 $. Sí en cada mes ganó 200 $ más que el mes anterior. ¿Cuántos meses tuvo el negocio?.
8) Se compra 1 artículo a pagar en 15 meses de este modo: 1 $ el 1er mes; 3 $ el 2do mes; 9 $ el 3er mes y así sucesivamente. Cuál es el importe del artículo.
9) Un hombre avanza en el 1er segundo de su carrera 6 mts. y en cada segundo posterior avanza
10) Hallar las longitudes de los lados de un triángulo, sabiendo que están en progresión aritmética de razón igual a
11) Una deuda debe ser pagada en 32 semanas; pagando 5 $ la 1ra semana, 8 $ la 2da semana, 11 $ la 3ra semana y así sucesivamente. Hallar el importe de la suma.
12) Los ahorros de los 3 primeros meses de una familia están en P.A. Sí en los 3 meses ha ahorrado 2.400 $ y el 1er mes ahorró la mitad de lo que ahorró el 2do mes. Cuánto ahorró cada mes.
13) El perímetro de un triángulo rectángulo es
14) Una piedra dejada caer libremente desde la azotea de un edificio recorre
15) Calcular las longitudes de los lados de un triángulo rectángulo, sabiendo que sus medidas expresadas en cm. son números que están en P.A. cuya razón es igual a 7.
16) Las ganancias mensuales de un comerciante durante 11 meses están en progresión aritmética. El 1er mes ganó 1.180 $ y el último 6.180 $. Cuánto más ganó en cada mes a contar del 2do mes, que en el anterior.
17) Determinar las longitudes de los lados de un triángulo rectángulo, sabiendo que están en P.A. de razón igual a 5.
18) Determinar el valor de "x" para que formen progresión aritmética de x ², (x + 2) ², (x + 3) ².
Juegos para practicar tus competencias y preparar las pruebas saber:
geometría
12 09 16
álgebra progresiones aritméticas, resumen de clase:
Progresiones aritméticas .Resumen de clase
Una progresión aritmética es una sucesión de números tales
que cada uno de ellos (salvo el primero) es igual al anterior más un número
fijo llamado diferencia que se representa por d.
8, 3, -2, -7, -12, ...
3 - 8 = -5
-2 - 3 = -5
-7 - (-2) = -5
-12 - (-7) = -5
d = −5.
Término general de una progresión aritmética
1. Si conocemos el 1er
término.
an
= a1 + (n - 1) · d
8, 3, -2, -7, -12,
..
an= 8 +
(n-1) (-5) = 8 -5n +5 = = -5n + 13
2. Si conocemos el valor que ocupa cualquier otro
término de la progresión.
an
= ak + (n - k) · d
a4= -7 y
d= -5
an = -7+ (n - 4) · (-5)= -7 -5n +20 = -5n
+ 13
Interpolación de términos en una progresión aritmética
Interpolar medios diferenciales o aritméticos entre dos
números, es construir una progresión aritmética que tenga por extremos los
números dados.
Sean los extremos a y b, y el número de medios
a interpolar m.
Interpolar tres medios aritméticos entre 8 y -12.
8, 3, -2, -7
, -12.
Suma de términos equidistantes de una progresión aritmética
Sean ai y aj dos términos
equidistantes de los extremos, se cumple que la suma de términos
equidistantes es igual a la suma de los extremos.
ai +
aj = a1 + an
a3
+ an-2
= a2 + an-1 = ... = a1 + an
8, 3, -2, -7, -12, ...
3 + (-7) = (-2) + (-2) = 8 + (-12)
-4 = -4 = -4
Suma de n términos consecutivos de una progresión aritmética
Calcular la suma de los primeros 5 términos de la progresión : 8, 3,
-2, -7, -12, ...
Ejercicios
de práctica de P.A
1) El cuarto término de una progresión aritmética
es 10, y el sexto es 16. Escribir la progresión.2) Escribir tres medios aritméticos entre 3 y 23.
3) Interpolar tres medios aritméticos entre 8 y -12.
4) El primer término de una progresión aritmética es -1, y el décimoquinto es 27. Hallar la diferencia y la suma de los quince primeros términos.
5) Hallar la suma de los quince primeros múltiplos de 5.
6) Hallar la suma de los quince primeros números acabados en 5.
7) Hallar la suma de los quince primeros números pares mayores que 5.
8) Hallar los ángulos de un cuadrilátero convexo, sabiendo que están en progresión aritmética, siendo d= 25º.
9) El cateto menor de un triángulo rectángulo mide
Matemáticas:
Notas del III periodo luego de las estrategias de apoyo. Hacer clic para descargar o ver:
9.1
Vídeos de ayuda para repasar problemas con ecuaciones cuadráticas.
Ecuaciones cuadráticas │pura, mixta, completa
Ecuaciones cuadráticas mixtas (parte 1)
Ecuaciones Cuadráticas por completación de
cuadrados - Ejercicio 2
Ecuaciones cuadráticas mixtas│compilado 2
discriminante ecuacion cuadratica
problema raices ecuacion cuadratica 101
problema ecuacion cuadratica 201
problema raices ecuacion cuadratica 201
planteo ecuacion cuadratica 101
álgebra 24 08 16
para repasar:
Resumen de clase
álgebra enlace para descargar la estrategia de apoyo del III periodo:
|
estadística 14 08 16
Enlace para presentar el quiz de estadística pictogramas:
álgebra 10 08 16
Talleres de ecuaciones cuadráticas
Resolver por factorización:
1. x2 - 5x + 6 = 0
2. 2x2 - 7x +3 = 0
3. -x2 + 7x − 10 = 0
4. x2 - 2x +1 = 0
5. x2 + x + 1 = 0
6. x2 - 4x + 4 = 0
7. 2x -3= 1- 2x+ x2
8x2 +
(7 − x)2 = 25
97x2 +
21x − 28 = 0
10−x2 +
4x − 7 = 0
11. 18= 6x + x(x-13)
126x2 −5x
+1 = 0
13. x2 +(x+2) =580
14. x2 −5x
-84=0
15. 4x2 −6x
+2=0
Enlace para el quiz de geometría
9.1
Resumen
de
SISTEMAS
DE ECUACIONES LINEALES
PALABRAS CLAVES: Ecuaciones, lineal, sistemas, 2x2, problemas, métodos, sustitución,
reducción, igualación, gráfico.
LOGROS:
Identifica,
representa y soluciona ecuaciones lineales.
Plantea
y soluciona problemas con ecuaciones.
Hace
uso adecuado de las tecnologías de la información y comunicación.
Pregunta generadora: ¿De qué forma aplico la solución de ecuaciones lineales en la vida
cotidiana?
SITUACION DE APRENDIZAJE
Cotidianamente
vas a encontrar que muchas de las situaciones que giran alrededor tuyo se
pueden plantear a través de una ecuación, por ejemplo:
En
mi clase están 35 alumnos. Nos han regalado por nuestro buen comportamiento 2
bolígrafos a cada chica y un cuaderno a cada chico. Si en total han sido 55
regalos, ¿cuántos chicos y chicas están en mi clase?
¿Cómo
plantearías una ecuación a esta situación?
¿Cuál
es la solución a la pregunta del problema?
Te
invito a que leas la siguiente información para que aprendas a plantear y
desarrollar ecuaciones lineales.
Lee
con atención:
Sistema de ecuaciones lineales
Toda
igualdad de la forma ax +by = c donde a, b, c Є R es una ecuación lineal con
dos incógnitas.
Cada
pareja ordenada de números reales que satisface esta ecuación es una solución
de ella.
Por
ejemplo, para encontrar las soluciones de la ecuación y – 3x = 2, se despeja y,
y luego se asignan valores arbitrarios a x.
De
esta forma, dando valores a x, se pueden obtener infinitos valores para y.Así,
se dice que la ecuación lineal y – 3x = 2 es una ecuación indeterminada.
Toda
ecuación lineal con dos incógnitas es una ecuación indeterminada.
Un
conjunto formado por dos o más incógnitas lineales es llamado sistemas de
ecuaciones lineales o sistemas de ecuaciones simultáneas.
Por
ejemplo, el conjunto
3x –
y = 7
2x +
y = 8
Es
un sistema 2x2, pues está formado por dos
ecuaciones con dos incógnitas. La solución de este sistema es la pareja (3,2)
ya que satisface las dos ecuaciones simultáneamente.
El
conjunto
3x –
2y + 3z = 16
x +
3y – 6z = -23
5x +
4y – 2z = -9
Es
un sistema 3x3, pues está formado por tres
ecuaciones con tres incógnitas. la solución de este sistema está dada por la
terna (1, -2, 3)
ACTIVIDADES
¿Conoces
como se soluciona sistemas de ecuaciones lineales?
Busca
la respuesta en la página: http://www.colombiaaprende.edu.co/recursos/skoool/algebra/sistemas_de_ecuaciones_lineales/index.html
Para
solucionar ecuaciones lineales se presentan varios métodos, entra a la página
Copia los métodos allí explicados en un
documento de Word, soluciona los ejercicios
Copia
en tu cuaderno el mapa conceptual que aparece en herramientas de andamiaje y
agrégale a cada método un ejemplo.
Observa
el video que se encuentra en la página http://matematicasies.comspip.php?article1691 sobre la solución grafica de
ecuaciones lineales.
Resuelve
los ejercicios del 1 al 28 planteados en la siguiente página http://www.matebrunca.com/Contenidos/Matematica/algebra/sistemasdeecuaciones.pdf
Preséntalos
resueltos en tu cuaderno en clase. Prepáralos para ser sustentados.
Resuelve
los siguientes problemas propuestos que encuentras en : http://www.monografias.com/trabajos58/ejercicio-ecuaciones-lineales/ejercicio-ecuaciones-lineales2.shtml
.
RECURSOS
BIBLIOGRAFIA Y CIBERGRAFIA
Matemática
grado noveno Editorial Santillana.
tomado de
álgebra 06 08 16
Luego de hacer el repaso , realizar el quiz virtual haciendo clic en:
estadística 05 08 16Luego de hacer el repaso , realizar el quiz virtual haciendo clic en:
Realizar el siguiente taller en el cuaderno para ser sustentado.
Taller de estadística
1.
Número de libros leídos por un grupo de
estudiantes en un año.
3 2 1 4 5 3 2 1 3 1
2 3 5 1 2 2 1 3 4 2
3 4 0 1 2 2 0 1 2 3
Elaborar la tabla de distribución de
frecuencias
Realizar los histogramas de frecuencias
Dibujar el diagrama circular
2.
Número de días que practico deporta a la
semana
4 2 3 1 3 7 1 0 3 2
6 2 3 3 4 6 3 4 3 6
Elaborar la tabla de distribución de
frecuencias
Realizar los histogramas de frecuencias
Dibujar el diagrama circular
3.
Número de llegadas tarde el colegio de un
grupo de 20 estudiantes.
4 5 7 5 8
3 9 6 4 5
7 5 8 4 3
10 6 6 3 3
Elaborar la tabla de distribución de
frecuencias
Realizar los histogramas de frecuencias
Dibujar el diagrama circular
4
Horas de estudio que dedican a la semana
para matemáticas
16 11 17 12 10 5 1 8 10 14
15 10 3
2 5 16 10 3 4 12
Elaborar la tabla de distribución de
frecuencias
Realizar los histogramas de frecuencias
Dibujar el diagrama circular
5.
Edad de un grupo de 30 personas que entran a un centro comercial.
24 3 29 6 5
17 25 24 36 42
30 16 14 12
8 4 8 37 32 40
37 26 28 15 17 41 20 18 27 42
Elaborar la tabla de distribución de
frecuencias
Realizar los histogramas de frecuencias
Dibujar el diagrama circular
6.
Se encuesta a 20 familias sobre el número de días que van a
hacer compras a la tienda.
1 2 2 4 6
1 6 1 2 3
5 2 6 3 1
4 1 6 1 2
Elaborar la tabla de distribución de
frecuencias
Realizar los histogramas de frecuencias
Dibujar el diagrama circular
7.
Pesos en kg de 20 recien nacidos.
2.8
3.2 3.8 2.5 2.7
3.0 2.6 1.8 3.3
2.9
2.9 3.5 3.0 3.1
2.2
3.7 1.9 2.6 3.5
2.3
Elaborar la tabla de distribución de
frecuencias
Realizar los histogramas de frecuencias
Dibujar el diagrama circular
estadística 17 07 16
Enlace para presentar el quiz virtual de estadística:
9.1
Si olvidó su clave , solicitarla con su nombre y grado
al correo :
jelkinvega@yahoo.es
¿Qué es un pictograma? resumen de clase
Un pictograma es un tipo de
gráfico cuya información se grafica a través de dibujos.
Por ejemplo:
María encuestó a sus compañeros
respecto a sus lugares preferidos para pasear. Con los datos, construyó el
siguiente pictograma.
Con estos datos podemos decir
que:
- 6 de sus compañeros prefieren el zoológico para pasear
- 2 de sus compañeros prefieren el parque para pasear
- 4 de sus compañeros prefieren el cine para pasear
- 8 de
sus compañeros prefieren el circo para pasear
- 6 de sus compañeros prefieren el museo para pasear
Además podemos decir que en el
curso de maría hay un total de 26 alumnos.
Ahora inténtalo tú.
El siguiente pictograma muestra
los goles anotados por un equipo de fútbol en 4 partidos.
Responde las siguientes
preguntas:
1- ¿En qué partido se anotaron
más goles?
2- ¿En qué partido se anotaron
menos goles?
3- ¿Cuántos goles menos se
anotaron en el 4° partido que en el 3° partido?
4- La suma de los goles del 2°
y 4°partido equivalen a los goles anotados en el ____________ partido.
5- ¿Cuántos goles más se
anotaron en el 3° partido que en el segundo partido?
______________ goles.
12 06 16
Taller de problemas de ecuaciones 2x2, para practicar.
1.
Juan compró un ordenador y un televisor por 2000 € y los
vendió por 2260 €.¿Cuánto le costó cada objeto, sabiendo que en la venta del
ordenador ganó el 10% y en la venta del televisor ganó el 15%?.
2.
El perímetro de un triángulo rectángulo mide
16 cm y su base es el triple de su
altura. Entonces su área es:
3.
Una granja tiene pavos y cerdos, en
total hay 58 cabezas y 168 patas. Entonces el número de cerdos y pavos que hay
es:
4.
En una empresa trabajan 60 personas. Usan gafas el 16% de
los hombres y el 20% de las mujeres. Si el número total de personas que usan
gafas es 11. Entonces el número de hombres y mujeres hay en la empresa es:
5.
Por la compra de dos electrodomésticos hemos pagado 3500
€. Si en el primero nos hubieran hecho un descuento del 10% y en el segundo un
descuento del 8% hubiéramos pagado 3170 €. Entonces el precio de cada artículo
es :
6.
Hallar dos números tales que la suma sus recíprocos sea 5
y la diferencia entre los recíprocos sea 1.
7.
Se tienen 120
euros en 33 billetes de 5 y de 2 euros. Entonces el número de billetes de 5 y
de 2 euros es:
8.
El doble de la suma de dos números es 32, y su diferencia
es cero. Hallar los números.
9.
Katy tiene el triple de la edad de Juan. Dentro de 15
años la edad de Katy será el doble de la edad de Juan. Entonces las edades
actuales son :
10.
Si la suma de dos números es -1, y su diferencia es 9.
Entonces los números son :
Ecuaciones simultáneas
por sustitución
reducción
http://www.colombiaaprende.edu.co/recursos/skoool/algebra/sistemas_de_ecuaciones_lineales/index.html
Solución de un Sistema de Ecuaciones Lineales de 2x2 por el Método Gráfico
Solución de un Sistema de 2x2 por el Método de Igualación
Solución de un Sistema de 2 x 2 por el Método de Eliminación
Solución de un Sistema de 2x2 por el Método de Sustitución
resumen en pdf
Ejercicios de practica:
álgebra aprendamos mientras descansamos:
La belleza está en
todas partes matemáticas
Las simetrías del universo | Documental Redes
Eduard Punset
El número de Oro - El Sello de Dios.
Donald en la tierra mágica de la matemática
APLICACIÓN DE LOS NÚMEROS EN LA VIDA DIARIA
geometría:Enlaces para repasar elementos del círculo y circunferencia:
Área de un Sector
Circular
Área de un trapecio circular o cuadrilátero
curvilíneo
Perímetro y área de un sector de corona
circular
Longitud de un arco dentro de una
circunferencia
Área circunferencia y sector circular: Cabra
fuera redil.
Problemas de aplicación de Geometría
sector circular
1. Una vaca está atada a la
esquina de un granero rectangular de 4 metros de ancho por 5 metros de largo,
con una cuerda de 6 metros. Determinar el área en la que la vaca puede pastar.
2. Calcular el área del
sector circular cuya cuerda es el lado de un triángulo equilátero inscrito
siendo 2 metros el radio de la circunferencia.
3. Si el área de un sector
circular de 90° es 4pi metros cuadrados. Calcular el radio del círculo al que pertenece,
la longitud del arco comprendido, el área del círculo y la longitud de la
circunferencia total.
4. Hallar el área de un
sector circular cuya cuerda es el lado de un cuadrado inscrito siendo 4 metros
el radio de la circunferencia
5. Determinar la longitud del
arco de circunferencia del Problema 4.
6. Un faro barre con su luz
un ángulo plano de 120° . Si el alcance máximo del faro es de 6 millas. Cuál es
la longitud máxima en millas y en metros
del arco correspondiente.
7. Los brazos de un columpio
miden 1.5 metros de largo y pueden describir como máximo un ángulo de 140°.
Calcular el espacio recorrido por el asiento del columpio cuando el ángulo
descrito en su balanceo es el máximo.
Enlace para descargar la estrategia de apoyo del II periodo:
9º
Repaso de ángulos de la circunferencia:
07 05 16 Álgebra
Aplicaciones de la función lineal:
Álgebra 28 04 16
Resumen de relaciones y funciones
Relaciones y funciones
Entender los conceptos de Relación y
de Función es de suma importancia en
Matemática.
Para lograr esa comprensión es necesario adentrarnos
en la noción de Correspondencia, ya que esta tiene un papel
fundamental en las relaciones y funciones.
Lo primero es entender que Correspondencia es
equivalente a Relación. En nuestra lengua, decir “en relación a”, es
equivalente a decir “corresponde a”.
Ejemplos:
En una tienda comercial, cada artículo está
relacionado con su precio; o sea, a cada artículo le
corresponde un precio.
En la guía telefónica, cada cliente está
relacionado con un número; o sea, a cada nombre de la guía le
corresponde un número.
Definición matemática
de Relación y de Función
En matemática, Relación es la
correspondencia de un primer conjunto, llamado Dominio, con un
segundo conjunto, llamado Recorrido, contradominio o Rango, de
manera que a cada elemento del Dominio le corresponde uno o más elementos del
Recorrido o Rango.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
De las definiciones anteriores podemos deducir que
todas las funciones son relaciones, pero no
todas las relaciones son funciones.
También debemos agregar que toda ecuación es una Relación,
pero no toda ecuación es una Función.
Todas las Relaciones pueden ser
graficadas en el Plano Cartesiano.
Ver: Plano Cartesiano
Dados dos conjuntos A y B una relación definida de A
en B es un conjunto de parejas ordenadas (par ordenado) que hacen
verdadera una proposición; dicho de otro modo, una relación es cualquier
subconjunto del producto cartesiano A x B
Ejemplo 1.
Si A = {2, 3} y B = {1, 4, 5}, encontrar tres
relaciones definidas de A en B.
Solución
El producto cartesiano de A x B está conformado por
las siguientes parejas o pares ordenados:
A x B = {(2, 1), (2, 4), (2, 5), (3, 1), (3, 4), (3, 5)}
Y cada uno de los siguientes conjuntos corresponde a
relaciones definidas de A en B:
R1 = {(2, 1), (3, 1)}
R2 = {(2, 4), (2, 5), (3, 4), (3, 5)}
R3 = {(2, 4), (3, 5)}
La relación R1 se puede definir como el conjunto de
pares cuyo segundo elemento es 1, esto es, R1 = {(x, y)
/ y = 1}.
La relación R2 está formada por los pares cuyo primer
componente es menor que el segundo componente, R2 = {(x, y)
/ x < y}
Y la relación R3 está conformada por todos los pares
que cumplen con que el segundo componente es dos unidades mayor que el primer
componente, dicho de otro modo, R3 = {(x, y) / y =
x + 2}
Así, se puede continuar enumerando relaciones
definidas a partir de A x B. Como se puede ver, la regla que define la relación
se puede escribir mediante ecuaciones o desigualdades que relacionan los valores
de x e y. Estas reglas son un medio conveniente
para ordenar en pares los elementos de los dos conjuntos.
Ejemplo 2.
Dados los conjuntos C = {1, –3} y D = {2, 3, 6},
encontrar todos los pares ordenados (x, y) que satisfagan la
relación
R = {(x, y) / x + y =
3}
Solución
El producto cartesiano de C x D está formado por los
siguientes pares ordenados
C x D = {(1, 2),
(1, 3), (1, 6), (–3, 2), (–3, 3), (–3, 6)}
Las parejas ordenadas que satisfacen que la suma de
sus componentes sea igual a 3 son:
R
= {(1, 2), (–3, 6)}
Toda relación queda definida si se conoce el conjunto
de partida, el conjunto de llegada y la regla mediante la cual se asocian los
elementos. En el ejemplo anterior, el conjunto de partida corresponde al
conjunto C, el conjunto de llegada es el conjunto D y
la expresión x + y = 3 es la regla que
asocia los elementos de los dos conjuntos.
Dominio y rango de una relación
El dominio de una relación es el
conjunto de preimágenes; es decir, el conjunto formado por los
elementos del conjunto de partida que están relacionados. Al conjunto de imágenes,
esto es, elementos del conjunto de llegada que están relacionados, se le
denomina recorrido o rango.
Ejemplo 3
Sea A = {1, 2, 3, 4} y B = {4, 5, 6, 7, 8} y R
la relación definida de A en B determinada por la regla “y es
el doble de x” o “y = 2x”, encontrar
dominio y rango de la relación.
Solución
El total de pares ordenados que podemos formar, o
producto cartesiano es:
A x B = {(1, 4), (1, 5), (1, 6), (1, 7), (1, 8),
(2, 4), (2, 5), (2, 6), (2, 7), (2, 8), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8),
(4, 4), (4, 5), (4, 6), (4, 7), (4, 8)}
Pero los pares que pertenecen a la relación R (y = 2x)
son solo:
R = {(2, 4), (3, 6), (4, 8)}
En esta relación vemos que: “4 es el doble de 2”; esto
es, “4 es la imagen de 2 bajo R”, dicho de otro modo, “2 es preimagen de 4”.
Así, el dominio y rango son:
D = {2, 3, 4}
Rg = {4, 6, 8}
Según lo que vemos, ¿Qué relación hay entre el Dominio
y el conjunto de partida?
En el Dominio falta el elemento 1 del conjunto de
partida, por lo tanto el Dominio es un subconjunto de A.
Otra pregunta: ¿Todo elemento del conjunto de llegada
es elemento del rango?
La respuesta es no, pues en el rango faltan el 5 y el
7.
Representación gráfica de las relaciones
Los pares ordenados se pueden representar gráficamente
por medio de diagramas sagitales o por medio de puntos en
el plano cartesiano. Veamos el siguiente ejemplo.
Ejemplo 4
Si A = {1, 2, 3, 4, 5} y B = {1, 3, 5, 7, 9}
y R la relación definida por la regla
R = {(x, y) / y =
2x + 1}, graficar R.
Solución
Los pares ordenados que pertenecen a la relación
(que cumplen con y = 2x + 1) son:
R
= {(1, 3), (2, 5), (3, 7), (4, 9)}
Fuente Internet:
Es propiedad: www.profesorenlinea.cl
- Registro N° 188.540
Tipos de relaciones y funciones 1
Amplia tus conceptos de funciones
Ejercicios interactivos para que te autovalues:
coordenadas
representación
de puntos
tablas
de valores
representación
grafica
características
funcion
función
lineal
función
afin
función
constante
para
ampliar mas
graficas
de funciones
Descargar el archivo para ampliar el tema:
Enlace para presentar el quiz virtual del Teorema de Pitágoras:
Geometría
Realizar en el cuaderno las siguientes aplicaciones del teorema de Pitágoras:
1 La
hipotenusa de un triángulo rectángulo mide 30 cm y la proyección de un cateto
sobre ella 10.8 cm. Hallar el otro cateto.
2En
un triángulo rectángulo, las proyecciones de los catetos sobre la hipotenusa
miden 4 y 9 metros. Calcular la altura relativa a la hipotenusa.
3 La
hipotenusa de un triángulo rectángulo mide 405.6 m y la proyección de un
cateto sobre ella 60 m. Calcular:
1 Los
catetos.
2 La
altura relativa a la hipotenusa.
3 El
área del triángulo.
4 Calcular
los lados de un triángulo rectángulo sabiendo que la proyección de uno de los
catetos sobre la hipotenusa es 6 cm y la altura relativa de la misma es raíz de 24 cm.
cm.
5 Una
escalera de 10 m de longitud está apoyada sobre la pared. El pie de la
escalera dista 6 m de la pared. ¿Qué altura alcanza la escalera sobre la
pared?
6 Determinar
el lado de un triángulo equilátero cuyo perímetro es igual al de un cuadrado de
12 cm de lado. ¿Serán iguales sus áreas?
7 Calcular
el área de un triángulo equilátero inscrito en una circunferencia de radio
6 cm.
8 Determinar
el área del cuadrado inscrito en una circunferencia de longitud 18.84 m.
9 En
un cuadrado de 2 m de lado se inscribe un círculo y en este círculo un
cuadrado y en este otro círculo. Hallar el área comprendida entre el último
cuadrado y el último círculo.
10 El
perímetro de un trapecio isósceles es de 110 m, las bases miden 40 y
30 m respectivamente. Calcular los lados no paralelos y el área.
11 Si
los lados no paralelos de un trapecio isósceles se prolongan, quedaría formado
un triángulo equilátero de 6 cm de lado. Sabiendo que el trapecio tiene la
mitad de la altura del triángulo, calcular el área del trapecio.
12 El
área de un cuadrado es 2304 cm2. Calcular el área del hexágono
regular que tiene su mismo perímetro.
13 En
una circunferencia de radio igual a 4 m se inscribe un cuadrado y sobre
los lados de este y hacia el exterior se construyen triángulos equiláteros.
Hallar el área de la estrella así formada.
14 A
un hexágono regular
4 cm de lado se le inscribe una circunferencia y se le circunscribe otra.
Hallar el área de la corona circular así formada.
15 En
una circunferencia una cuerda de 48 cm y dista 7 cm del centro.
Calcular el área del círculo.
16 Los
catetos de un triángulo inscrito en una circunferencia miden 22.2 cm y
29.6 cm respectivamente. Calcular la longitud de la circunferencia y el
área del círculo.
17 Calcular
el lado de un triángulo equilátero inscrito en una circunferencia de 10 cm
de radio.
18 Sobre
un círculo de 4 cm de radio se traza un ángulo central de 60°. Hallar el
área del segmento circular comprendido entre la cuerda
que une los extremos de los dos radios y su arco correspondiente.
19 Dado
un triángulo equilátero de 6 m de lado, hallar el área de uno de los
sectores determinado por la circunferencia circunscrita y por los radios que
pasan por los vértices.
20 Calcular
el área de la corona circular determinada por las circunferencias inscrita y
circunscrita a un cuadrado de 8 m de diagonal.
22 04 2016
Resumen de relaciones y funciones:
Entender
los conceptos de Relación y de Función es de suma importancia en
Matemática.
Para
lograr esa comprensión es necesario adentrarnos en la noción de Correspondencia,
ya que esta tiene un papel fundamental en las relaciones y funciones.
Lo
primero es entender que Correspondencia es equivalente a Relación. En
nuestra lengua, decir “en relación a”, es equivalente a decir “corresponde a”.
Ejemplos:
En una
tienda comercial, cada artículo está relacionado con su precio; o sea, a
cada artículo le corresponde un precio.
En la
guía telefónica, cada cliente está relacionado con un número; o sea, a
cada nombre de la guía le corresponde un número.
Definición matemática de Relación y de Función
En
matemática, Relación es la correspondencia de un primer conjunto,
llamado Dominio, con un segundo conjunto, llamado Recorrido o Rango,
de manera que a cada elemento del Dominio le corresponde uno o más elementos
del Recorrido o Rango.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
De las
definiciones anteriores podemos deducir que todas las funciones son relaciones,
pero no todas las relaciones son funciones.
También
debemos agregar que toda ecuación es una Relación, pero no toda ecuación
es una Función.
Todas las
Relaciones pueden ser graficadas en el Plano Cartesiano.
Ver: Plano Cartesiano
Dados dos
conjuntos A y B una relación definida de A en B es un conjunto de parejas
ordenadas (par ordenado) que hacen verdadera una proposición; dicho de
otro modo, una relación es cualquier subconjunto del producto cartesiano A x B
Ejemplo
1.
Si A =
{2, 3} y B = {1, 4, 5}, encontrar tres relaciones definidas de A en B.
Solución
El
producto cartesiano de A x B está conformado por las siguientes parejas o pares
ordenados:
A x B = {(2, 1), (2, 4), (2, 5), (3, 1), (3, 4), (3, 5)}
Y cada
uno de los siguientes conjuntos corresponde a relaciones definidas de A en B:
R1 = {(2, 1), (3, 1)}
R2 = {(2, 4), (2, 5), (3, 4), (3, 5)}
R3 = {(2, 4), (3, 5)}
La
relación R1 se puede definir como el conjunto de pares cuyo segundo elemento es
1, esto es, R1 = {(x, y) / y = 1}.
La
relación R2 está formada por los pares cuyo primer componente es menor que el
segundo componente, R2 = {(x, y) / x < y}
Y la
relación R3 está conformada por todos los pares que cumplen con que el segundo
componente es dos unidades mayor que el primer componente, dicho de otro modo,
R3 = {(x, y) / y = x + 2}
Así, se
puede continuar enumerando relaciones definidas a partir de A x B. Como se
puede ver, la regla que define la relación se puede escribir mediante ecuaciones
o desigualdades que relacionan los valores de x
e y. Estas reglas son un medio conveniente para ordenar en pares
los elementos de los dos conjuntos.
Ejemplo
2.
Dados los
conjuntos C = {1, –3} y D = {2, 3, 6}, encontrar todos los pares ordenados (x,
y) que satisfagan la relación
R = {(x, y) / x + y = 3}
Solución
El
producto cartesiano de C x D está formado por los siguientes pares ordenados
C x D = {(1, 2),
(1, 3), (1, 6), (–3, 2), (–3, 3), (–3, 6)}
Las
parejas ordenadas que satisfacen que la suma de sus componentes sea igual a 3
son:
R
= {(1, 2), (–3, 6)}
Toda
relación queda definida si se conoce el conjunto de partida, el conjunto de
llegada y la regla mediante la cual se asocian los elementos. En el ejemplo
anterior, el conjunto de partida corresponde al conjunto C, el conjunto
de llegada es el conjunto D y la expresión x + y
= 3 es la regla que asocia los elementos de los dos conjuntos.
Dominio y rango de una relación
El dominio
de una relación es el conjunto de preimágenes; es decir, el conjunto
formado por los elementos del conjunto de partida que están relacionados. Al
conjunto de imágenes, esto es, elementos del conjunto de llegada que
están relacionados, se le denomina recorrido o rango.
Ejemplo
3
Sea A =
{1, 2, 3, 4} y B = {4, 5, 6, 7, 8} y R la relación definida de A en B
determinada por la regla “y es el doble de x” o “y
= 2x”, encontrar dominio y rango de la relación.
Solución
El total
de pares ordenados que podemos formar, o producto cartesiano es:
A x B
= {(1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (2, 4), (2, 5), (2, 6), (2,
7), (2, 8), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (4, 4), (4, 5), (4, 6), (4,
7), (4, 8)}
Pero los
pares que pertenecen a la relación R (y = 2x) son solo:
R = {(2, 4), (3, 6), (4, 8)}
En esta
relación vemos que: “4 es el doble de 2”; esto es, “4 es la imagen de 2 bajo
R”, dicho de otro modo, “2 es preimagen de 4”.
Así, el
dominio y rango son:
D = {2, 3, 4}
Rg = {4, 6, 8}
Según lo
que vemos, ¿Qué relación hay entre el Dominio y el conjunto de partida?
En el
Dominio falta el elemento 1 del conjunto de partida, por lo tanto el Dominio es
un subconjunto de A.
Otra
pregunta: ¿Todo elemento del conjunto de llegada es elemento del rango?
La
respuesta es no, pues en el rango faltan el 5 y el 7.
Representación gráfica de las relaciones
Los pares
ordenados se pueden representar gráficamente por medio de diagramas
sagitales o por medio de puntos en el plano cartesiano. Veamos el
siguiente ejemplo.
Ejemplo 4
Si
A = {1, 2, 3, 4, 5} y B = {1, 3, 5, 7, 9} y R la relación definida por la
regla
R = {(x,
y) / y = 2x + 1}, graficar R.
Solución
Los pares
ordenados que pertenecen a la relación (que cumplen con y = 2x + 1) son:
R
= {(1, 3), (2, 5), (3, 7), (4, 9)}
Y la
gráfica correspondiente es la siguiente:
Relaciones y Funciones
17 04 2016
Enlace para descargar el libro" el hombre que calculaba"
El
hombre que calculaba
Enlaces para el quiz de geometría , presentar hasta el miercoles
teorema de thales
16 04 2016
Enlace para el quiz virtual de Estadística:
Bienvenidos
al 2016
12 04 2016 Geometría
11 04 2016
Estadística
Resumen de clase:
Frecuencia relativa
Enlaces para el quiz de geometría , presentar el sábado,
https://www.thatquiz.org/es/classtest?ZO6MY4EO
28 03 2016
Resumen de la clase de estadística
20 03 2016
Invitación: ingresa al enlace para inscribirte:
http://www.superate.gov.co/
08 03 2016
Enlaces para las estrategias de apoyo.
Esto le servirá para preparar la evaluación de recuperación.
Descargar desde el enlace, el resumen de semejanza de triángulos. luego de leer realizar las autoevaluaciones.
Hacer clic en :
11 11 2016
Enlaces para presentar el quiz de
Enlaces para descargar o ver los talleres de estrategias de apoyo 2015
Enlace para descargar el taller de apoyo del IV periodo:
27 10 20
Autoevaluación del estudiente IV periodo:
07 10 20
Enlaces para repasar Progresiones geométricas:
Progresiones Geométricas -
Ejercicio 1
Progresiones Geométricas -
Ejercicio 2
Progresiones Geométricas -
Ejercicio 3
Puedes practicar P.A. y preparar la evaluación ,realizando las siguientes autoevaluaciones:
12 09 2015
Progresiones aritméticas (P.A.), resumen de clase:
Progresiones Aritméticas -
Ejercicio 1
Progresiones Aritméticas -
Ejercicio 2
Progresiones Aritméticas -
Ejercicio 4
Progresiones Aritméticas -
Ejercicio 5
Progresiones Aritméticas -
Ejercicio 4
08 09 20
31 08 2015
Ecuaciones logarítmicas resumen de clase:
Log 3(x+4)+Log3(x-4)=2
2Log2x2 -2Log3(-x)=4
Log 3[(x+4)(x-4)] = 2 Log2(x2)2-Log2(-x)2=4
Log 3(x2-16) = 2 Log 2x4 - Log 2x2 = 4
x2-16 = 32 Log 2(x4 /x2)=4
x2 = 9 + 16 x2 = 24
x2 = 25 x2 = 16
x = ± 5 x = ± 4
En la primer ecuación, solo se verifica la solución positiva: x=5, mientras que en la segunda solo la negativa: x=-4
(Log 2x)2-5Log2x+4=0
Cambio de variable:
z = Log2x
Ecuaciones Logarítmicas
https://www.youtube.com/watch?v=gSlkeCgTSuk
Ecuaciones Logarítmicas - Ejercicio 1
https://www.youtube.com/watch?v=riqZcExsvcE
Ecuaciones Logarítmicas - Ejercicio 2
https://www.youtube.com/watch?v=1qVTH0Dr4C0
Ecuaciones Logarítmicas - Ejercicio 3
https://www.youtube.com/watch?v=UcgsO70f5sU
Ecuaciones Logarítmicas - Ejercicio 4
https://www.youtube.com/watch?v=LW_sP5jDBQA
Ecuaciones Logarítmicas - Ejercicio 5
https://www.youtube.com/watch?v=g3KhxSJVcSg
Ecuaciones Logarítmicas - Ejercicio 6
https://www.youtube.com/watch?v=EaxI046b7t8
Ecuaciones Logarítmicas - Ejercicio 7
https://www.youtube.com/watch?v=ZF47GJUB6iU
Ecuaciones Logarítmicas - Ejercicio 8
https://www.youtube.com/watch?v=5KWcFn1jWDs
Ecuaciones Logarítmicas - Ejercicio 9
https://www.youtube.com/watch?v=_dDp9BoFODI
Ecuaciones Logarítmicas - Ejercicio 10
https://www.youtube.com/watch?v=yLoA7aEGJz0
Ecuaciones Logarítmicas - Ejercicio 11
https://www.youtube.com/watch?v=dm8d4yUTqJ0
Ecuaciones Logarítmicas - Ejercicio 12
Ecuaciones Logarítmicas - Ejercicio 13
https://www.youtube.com/watch?v=f1_ACPdtA-Q
Ecuaciones Logarítmicas - Ejercicio 14
https://www.youtube.com/watch?v=dApslxUJMhU
22 08 20
Autoevaluación del estudiante:
Autoevaluación III periodo
21 08 20
Enlaces para el
19 08 20
Resumen de logaritmos y sus propiedades(videos):
Logaritmos 02 matemáticas
Logaritmos 03 matemáticas
Logaritmos 04 matemáticas
08 08 2015
04 07 2015
Recomendaciones para resolver problemas
100 problemas de matemáticas que todo estudiante de bachillerato debe saber y conocer.
Descargar de:
clic en DOWNLOAD NOW
http://www32.zippyshare.com/v/s2eO3ER0/file.html
enlace activo 30 días 03 05 20
28 04 20
Enlaces que les pueden servir para comprobar gráficas de funciones on line:
25 04 2015
Resumen de relaciones y funciones
Tipos de relaciones y
funciones 1
22 04 20
18 04 20
06 03 20
Autoevaluación del estudiante:
Autoevaluación del I periodo
03 03 2015
El código Dane de Sorjuana es:
29 02 2015
Enlaces para practicar racionalización:
12 04 2016 Geometría
Leer el tema y
resumir en el cuaderno: teorema del cateto en el enlace:
Luego realizar la siguiente autoevaluación :
Leer el tema y resumir en el cuaderno : teorema de la altura
en el enlace:
y luego practicar con la siguiente autoevaluación:
Leer el resumen del teorema de Pitágoras en el enlace:
Y luego practicar con la siguiente autoevaluación:
Estadística
Resumen de clase:
Distribución de frecuencias
y tablas
Una distribución de
frecuencias o tabla de frecuencias es una ordenación en
forma de tabla de los datos estadísticos,
asignando a cada dato su frecuencia correspondiente.
Tipos de frecuencia
Frecuencia absoluta
La frecuencia absoluta es
el número de veces que aparece un determinado valoren
un estudio estadístico.
Se representa por fi.
La suma de las
frecuencias absolutas es igual al número total de datos, que se
representa por N.
f1+f2+f3+….+fn=N
Para indicar resumidamente estas
sumas se utiliza la letra griega Σ (sigma mayúscula) que se
lee suma o sumatoria.
La frecuencia relativa es
el cociente entre la frecuencia absoluta de
un determinado valor y el número total de datos.
Se puede expresar en tantos por
ciento y se representa por ni.
ni=fi/N
La suma de las frecuencias
relativas es igual a 1.
Frecuencia absoluta acumulada
La frecuencia acumulada es
la suma de las frecuencias absolutas de todos los valores
inferiores o iguales al valor considerado.
Se representa por Fi.
Frecuencia relativa acumulada
La frecuencia relativa
acumulada es el cociente entre la frecuencia
acumulada de un determinado valor y el número
total de datos. Se puede expresar en tantos por ciento. Ni
Ejemplo
Durante el mes de julio, en una
ciudad se han registrado las siguientes temperaturas máximas:
32, 31, 28, 29, 33, 32, 31, 30,
31, 31, 27, 28, 29, 30, 32, 31, 31, 30, 30, 29, 29, 30, 30, 31, 30, 31, 34, 33,
33, 29, 29.
En la primera columna de la tabla
colocamos la variable ordenada de menor a mayor, en la segunda hacemos el
recuento y en la tercera anotamos la frecuencia absoluta.
xi
|
Recuento
|
fi
|
Fi
|
ni
|
Ni
|
27
|
I
|
1
|
1
|
0.032
|
0.032
|
28
|
II
|
2
|
3
|
0.065
|
0.097
|
29
|
6
|
9
|
0.194
|
0.290
|
|
30
|
7
|
16
|
0.226
|
0.516
|
|
31
|
8
|
24
|
0.258
|
0.774
|
|
32
|
III
|
3
|
27
|
0.097
|
0.871
|
33
|
III
|
3
|
30
|
0.097
|
0.968
|
34
|
I
|
1
|
31
|
0.032
|
1
|
31
|
1
|
Este tipo de tablas de frecuencias se
utiliza con variables discretas.
Practica lo estudiado, con las siguientes autoevaluaciones:
tipos de
variables
tablas
estadísticas
Enlaces para el quiz de geometría , presentar el sábado,
teorema de thales
28 03 2016
Resumen de la clase de estadística
Recolección de datos
1.
La recolección de datos se refiere al uso de una gran diversidad
de técnicas y herramientas que pueden ser utilizadas por el
analista para desarrollar los sistemas de información, los cuales pueden ser la entrevistas, la encuesta, el cuestionario, la observación, el diagrama de flujo y el diccionario de datos.
Todas estos instrumentos se aplicará en un momento en particular, con la
finalidad de buscar información que será útil a una investigación en común. En la presente
investigación trata con detalle los pasos que se debe seguir en el proceso de recolección de datos, con las técnicas ya antes nombradas.
Los analistas utilizan una variedad de métodos a fin de recopilar los datos sobre una situación
existente, como entrevistas, cuestionarios, inspección de registros (revisión en el sitio) y
observación. Cada uno tiene ventajas y desventajas. Generalmente, se utilizan
dos o tres para complementar el trabajo de cada una y ayudar a asegurar una
investigación completa.
Las entrevistas se utilizan para recabar información en forma verbal, a
través de preguntas que propone el analista. Quienes responden pueden ser
gerentes o empleados, los cuales son usuarios actuales del sistema existente, usuarios potenciales del sistema
propuesto o aquellos que proporcionarán datos o serán afectados por la
aplicación propuesta. El analista puede entrevistar alpersonal en forma individual o en grupos algunos analistas prefieren este método a las otras técnicas que se estudiarán más
adelante. Sin embargo, las entrevistas no siempre son la mejor fuente de datos
de aplicación.
Dentro de una organización, la entrevistas es la técnica más
significativa y productiva de que dispone el analista para recabar datos. En
otras palabras, la entrevistas es un intercambio de información que se efectúa
cara a cara. Es un canal de comunicación entre el analista y la organización;
sirve para obtener información acerca de las necesidades y la manera de
satisfacerlas, así como concejo y comprensión por parte del usuario para toda
idea o método nuevos. Por otra parte, la entrevista ofrece al analista una excelente
oportunidad para establecer una corriente de simpatía con el personal usuario,
lo cual es fundamental en transcurso del estudio.
Preparación de la Entrevista
1. Determinar la posición
que ocupa de la organización el futuro entrevistado, sus responsabilidades
básicas, actividades, etc. (Investigación).
4. Elegir un lugar donde se
puede conducir la entrevista con la mayor comodidad (Sicología).
Conducción de la Entrevista
2. Explicar la función propietaria como analista y la función que se
espera conferir al entrevistado. (Imparcialidad).
3. Hacer preguntas
específicas para obtener respuestas cuantitativas (Hechos).
4. Evitar las preguntas que
exijan opiniones interesadas, subjetividad y actitudes similares (habilidad).
5. Evitar el cuchicheo y
las frases carentes de sentido (Claridad).
7. Conservar el control de la entrevista, evitando las divagaciones y
los comentarios al margen de la cuestión.
8. Escuchar atentamente lo
que se dice, guardándose de anticiparse a las respuestas (Comunicación).
Secuela de la Entrevista
2. Entregar una copia al
entrevistado, solicitando su conformación, correcciones o adiciones.
(Profesionalismo).
Recabar datos mediante la Entrevista
La entrevista es una forma de conversación, no de interrogación, al
analizar las características de los sistemas con personal seleccionado
cuidadosamente por sus conocimientos sobre el sistema, los analistas pueden
conocer datos que no están disponibles en ningún otra forma.
En las investigaciones de sistema, las formas cualitativas
y cuantitativas de la información importantes. La información cualitativa está
relacionada con opinión, política y descripciones
narrativas de actividades o problemas, mientras que las descripciones
cuantitativas tratan con números frecuencia, o cantidades. A menudo las
entrevistas pueden ser la mejor fuente de información cualitativas, los otros
métodos tiende a ser más útiles en la recabación de datos cuantitativos.
Son valiosas las opiniones, comentarios, ideas o sugerencia en relación a
como se podría hacer el trabajo; las entrevistas a veces es la mejor forma para
conocer las actividades de las empresas. La entrevista pueden descubrir
rápidamente malos entendidos, falsa expectativa o incluso resistencia potencial para las aplicaciones
de desarrollo; más aún, a menudo es más fácil
calendarizar una entrevista con los gerentes de alto nivel, que pedirle que
llenen cuestionario.
Determinación del tipo de Entrevista
La estructura de la entrevista varia. Si el objetivo de la entrevista radica en adquirir
información general, es conveniente elaborar una serie de pregunta sin
estructura, con una sesión de preguntas y respuesta libres
Las entrevistas estructuradas utilizan pregunta estandarizada. El formato
de respuestas para las preguntas pueden ser abierto o cerrado; las preguntas
para respuestas abierta permiten a los entrevistados dar cualquier respuesta
que parezca apropiado. Pueden contestar por completo con sus propias palabras.
Con las preguntas para respuesta cerradas se proporcionan al usuario un
conjunto de respuesta que se pueda seleccionar. Todas las personas que
respondes se basan en un mismo conjunto de posible respuestas.
Los analistas también deben dividir el tiempo entre desarrollar preguntas
para entrevistas y analizar respuesta. La entrevista no estructurada no
requiere menos tiempos de preparación, porque no necesita tener por anticipado
las palabras precisas de las preguntas. Analizar las respuestas después de la
entrevista lleva más tiempo que con la entrevista estructuradas. El mayor costo radica en la preparación, administración y análisis de las entrevistas
estructuradas para pregunta cerradas.
Ejemplos de las preguntas abiertas y cerradas en la entrevista estructurada
FORMA DE PREGUNTA ABIERTA
|
FORMA DE PREGUNTA CERRADA
|
Ejemplo: obtener la información sobre las características de diseños
críticas para los empleados.
" algunos empleados han sugerido que la mejor forma para hacer
eficiente el procesamiento de pedidos es instalar un sistema de computadora que maneje todos los
cálculos..."
bajo estas circunstancias ¿ apoyaría usted el desarrollo de un sistema de
este tipo?.
|
Ejemplo: obtener la información sobre las
" La experiencia le ha proporcionado una amplia visión en cuanto a
la forma en la que la empresa maneja los pedidos..." Me
gustaría que usted contestara algunas preguntas específicas en relación en lo
anterior:
-¿Qué etapas trabajas bien?¿cuáles no
-¿En donde se presenta la mayor parte del problema?
- ¿Cuándo ocurre un atraso, cómo se maneja?
Entre otros
|
Selección de Entrevistados
Realizar entrevistas toma tiempo; por lo tanto no es posible utilizar este
método para recopilar toda la información que se necesite en la investigación; incluso el analista debe verificar los
datos recopilados utilizando unos de los otros métodos de recabación de datos.
La entrevista se aplican en todos los niveles gerencial y de empleados y
dependa de quien pueda proporcionar la mayor parte de la información útil para
el estudio los analistas que estudian la administración de inventarios pueden entrevistar a los
trabajadores del embarque y de recepción, al personal de almacén y a los supervisores de los diferentes turnos,
es decir. Aquellas personas que realmente trabajan en el almacén, también
entrevistarán a los gerentes más importante.
Realización de Entrevista
La habilidad del entrevistador es vital para el éxito en la búsqueda de hecho por medio de la
entrevista. Las buenas entrevista depende del conocimiento del analista tanto de la preparación
del objetivo de una entrevista específica como de las preguntas por realizar a
una persona determinada.
El tacto, la imparcialidad e incluso la vestimenta apropiada ayudan a
asegurar una entrevista exitosa. La falta de estos factores puede reducir
cualquier oportunidad de éxito. Por ejemplo, analista que trabaja en la
aplicación enfocada a la reducción de errores (captado por la gerencia de alto nivel) probablemente no
tendría éxito si llegara a una oficina de gerencia de nivel medio con la presentación
equivocada, ejemplo "Estamos aquí para resolver su problema".
A través de la entrevista, los analistas deben preguntarse a sí mismo las
siguientes preguntas:
·
¿Qué es lo que me está diciendo la persona?
·
¿Por qué me lo está diciendo a mí ?
·
¿Qué está olvidando?
·
¿Qué espera está persona que haga yo?
Entrevista estructurada
|
Entrevista no estructurada
|
|
VENTAJAS
|
-Asegura la elaboración uniforme de las preguntas para todos los que van
a responder.
-Fácil de administrar y evaluar.
-Resulta en entrevistas más pequeñas.
|
-El entrevistador tiene mayor flexibilidad al realizar las preguntas
adecuadas a quien responde.
-El entrevistador puede explotar áreas que surgen espontáneamente durante
la entrevista.
-Puede producir información sobre área que se minimizaron o en las que no
se pensó que fueran importantes.
|
DESVENTAJAs
|
-Alto costo de preparación.
-Los que responden pueden no aceptar un alto nivel en la estructura
y carácter mecánico de las preguntas.
-Un alto nivel en la estructura puede no ser adecuado para todas las
situaciones.
-El alto nivel en las estructuras reduce responder en forma
espontánea, así como la habilidad del entrevistador para continuar con
comentarios hacia el entrevistado.
|
-Puede utilizarse negativamente el tiempo, tanto de quien responde como
del entrevistador.
-Los entrevistadores pueden introducir sus sesgos en las preguntas o al
informar de los resultados.
-Puede recopilarse información extraña
-Toma tiempo extra recabar los hechos esenciales.
|
Se ha dicho que Estados Unidos ya no es una "sociedad industrial", sino una
"sociedad de información". Esto es, nuestros mayores problemas y
tareas ya no giran principalmente en la producción de bienes y servicios necesarios para nuestra
supervivencia y comodidad.
Nuestra "sociedad", requiere un rápido y preciso flujo de
información sobre las preferencias, necesidades y comportamiento de sus miembros. Es en respuesta a
esta necesidad crítica de información por el gobierno, el comercio y las instituciones sociales que tanta confianza se pone
en las encuestas.
Hoy en día la palabra "encuesta" se usa más frecuentemente para
describir un método de obtener información de una muestra de individuos. Esta "muestra" es
usualmente sólo una fracción de la población bajo estudio.
Por ejemplo, antes de una elección, una muestra de electores es interrogada
para determinar cómo los candidatos y los asuntos son percibidos por el
público… un fabricante hace una encuesta al mercado potencial antes de introducir un nuevo producto… una entidad del gobierno comisiona una
encuesta para obtener información para evaluar legislación existente o para
preparar y proponer nueva legislación.
No tan sólo las encuestas tienen una gran variedad de propósitos, sino que
también pueden conducirse de muchas maneras, incluyendo por teléfono, por correo o en persona.
Aún así, todas las encuestas tienen algunas características en común.
A diferencia de un censo, donde todos los miembros de la población son
estudiados, las encuestas recogen información de una porción de la población
de interés, dependiendo el tamaño de la muestra en el propósito
del estudio. En una encuesta bona fide, la muestra no es seleccionada
caprichosamente o sólo de personas que se ofrecen como voluntarios para
participar. La muestra es seleccionada científicamente de manera que cada
persona en la población tenga una oportunidad medible de ser seleccionada. De
esta manera los resultados pueden ser proyectados con seguridad de la muestra a la población mayor.
La información es recogida usando procedimientos estandarizados de manera que a
cada individuo se le hacen las mismas preguntas en
mas o menos la misma manera. La intención de la encuesta no es describir los
individuos particulares quienes, por azar, son parte de la muestra sino obtener
un perfil compuesto de la población.
Una "encuesta" recoge información de una "muestra." Una
"muestra" es usualmente sólo una porción de la población bajo
estudio.
El estándar de la industria para todas las organizaciones respetables que hacen encuestas es
que los participantes individuales nunca puedan ser identificados al reportar
los hallazgos. Todos los resultados de la encuesta deben presentarse en
resúmenes completamente anónimos, tal como tablas y gráficas estadísticas.
¿Cuán grande debe ser la muestra?
El tamaño de muestra requerido en una encuesta depende en parte de la calidad estadística necesaria para los establecer los
hallazgos; esto a su vez, está relacionado en cómo esos hallazgos serán usados.
Aún así, no hay una regla simple para el tamaño de muestra que pueda ser
usada en todas las encuestas. Mucho de esto depende de los recursos profesionales y fiscales
disponibles. Los analistas frecuentemente encuentran que una muestra de tamaño
moderado es suficiente estadística y operacionalmente. Por ejemplo,
las muy conocidas encuestas nacionales frecuentemente usan cerca de 1,000
personas para obtener información razonable sobre actitudes y opiniones
nacionales.
Cuando nos damos cuenta que una muestra apropiadamente seleccionada de sólo
1,000 individuos puede reflejar varias características de la población total,
es fácil apreciar el valor de usar encuestas para tomar decisiones
informadas en una sociedad compleja como la nuestra. Las encuestas
proveen medios rápidos y económicos de determinar la realidad
de nuestra economía y sobre los conocimientos,
actitudes, creencias, expectativas y comportamientos de las personas.
¿Quién lleva a cabo las Encuestas?
Todos conocemos sobre las encuestas de opinión pública que son reportadas
por los medios informativos. Por ejemplo, la Encuesta Gallup y la
Encuesta Harris emiten informes periódicos describiendo la opinión pública nacional sobre una amplia gama de
asuntos corrientes. Encuestas estatales y en las áreas metropolitanas,
frecuentemente con el apoyo económico de algún periódico o estación de televisión local, se reportan regularmente en
muchos lugares. Las cadenas mayores de radio y televisión, así como revistas nacionales de noticias también llevan a cabo encuestas e
informan sus resultados A pesar de esto, la gran mayoría de las encuestas no
son de opinión pública. La mayoría están dirigidas a un propósito
administrativo, comercial o científico. La gran variedad de asuntos con los que
tratan las encuestas se puede ilustrar con la siguiente lista de usos reales:
·
Las cadenas mayores de televisión confían en encuestas que le dicen cuántas
y qué tipo de personas ven sus programas.
·
Statistics Canadá lleva a cabo encuestas continuas de panel sobre niños (y sus familias) para estudiar sus necesidades
educativas y otras.
·
Es una buena práctica nunca identificar los participantes individuales. El
tamaño de la muestra depende de las metas estadísticas y de los recursos
disponibles para la encuesta.
·
Los fabricantes de automóviles usan encuestas para determinar cuán
satisfechos están las personas con sus autos.
·
El Negociado del Censo de los Estados Unidos lleva a cabo encuestas cada
mes para obtener información sobre empleo y desempleo en la nación.
·
La Agencia para la Política e Investigación sobre Cuidado de Salud de los Estados
Unidos auspicia una encuesta periódica para determinar cuanto dinero está gastando la gente en los distintos tipos de
cuidado médico.
·
Las autoridades de transportación local conducen encuestas para obtener
información
·
sobre los hábitos de viaje y transportación de las personas.
·
Las revistas y revistas profesionales usan encuestas para conocer qué leen
sus suscriptores.
·
Se llevan a cabo encuestas para conocer quien usa nuestros parques
nacionales y
·
otras facilidades recreativas.
Las encuestas proveen una fuente importante de conocimiento científico
básico. Economistas, sicólogos, profesionales de la salud y sociólogos llevan a
cabo encuestas para estudiar materias tales como los patrones de ingreso
y gastos en los hogares, las raíces del prejuicio étnico o racial, las implicaciones
de los problemas de salud en la vida de las personas, comparando el
comportamiento electoral y los efectos sobre la vida familiar de mujeres que
trabajan fuera del hogar.
¿Cuáles son algunos métodos comunes de Encuestas?
Las encuestas pueden ser clasificadas en muchas maneras. Una dimensión es
por tamaño y tipo de muestra. Las encuestas pueden ser usadas para estudiar
poblaciones humanas o no humanas (por ejemplo, objetos animados o
inanimados, animales, terrenos, viviendas). Mientras que
muchos de los principios son los mismos para todas las
encuestas, el foco aquí será en métodos para hacer encuestas a individuos.
Muchas encuestas estudian todas las personas que residen en un área
definida, pero otras pueden enfocar en grupos particulares de la población
-niños, médicos, líderes de la comunidad, los desempleados, o usuarios de un
producto o servicio particular. Las encuestas también
pueden ser conducidas con muestras locales, estatales o nacionales.
Las encuestas pueden ser clasificadas por su método de recolección de
datos. Las encuestas por correo, telefónicas y entrevistas en persona son las
más comunes. Extraer datos de récords médicos y otros se hace también con
frecuencia. En los métodos más nuevos de recoger datos, la información se entra
directamente a la computadora ya sea por un entrevistador
adiestrado o aún por la misma persona entrevistada. Un ejemplo bien conocido es
la medición de audiencias de televisión usando
aparatos conectados a una muestra de televisores que graban automáticamente los
canales que se observan.
Las encuestas son una fuente importante de conocimiento científico básico.
Las encuestas por correo, a través de entrevistas telefónicas o en persona son
las más comunes.
Las encuestas por correo pueden ser de costo relativamente bajo. Como con
cualquier otra encuesta, existen problemas en usar este método si no se presta
suficiente atención a obtener niveles altos de
cooperación. Estas encuestas pueden ser más efectivas cuando se dirigen a
grupos particulares, tal como suscriptores a una revista especializada o a miembros de una organización
profesional.
Las entrevistas telefónicas son una forma eficiente de recoger
ciertos tipos de datos y se están usando con cada vez mayor
frecuencia. Se prestan particularmente bien a situaciones donde es necesario
obtener resultados oportunos y cuando el largo de la encuesta es limitado.
Las entrevistas en persona en el hogar u oficina de un participante son
mucho más caras que las encuestas telefónicas o por correo. Estas pueden ser
necesarias especialmente cuando se debe recoger información compleja.
Algunas encuestas combinan varios métodos. Por ejemplo, una encuestadora
puede usar el teléfono para identificar participantes elegibles (tal como
localizar individuos mayores elegibles para Medicare) y luego hacer cita para
una entrevista en persona.
¿Qué preguntas hacemos en una Encuesta?
Podemos clasificar las encuestas también por su contenido. Algunas
encuestas enfocan en las opiniones y actitudes (tal como las encuestas
pre-eleccionarias), mientras que otras se preocupan por características o
comportamiento reales (tal como la salud de las personas, vivienda, gastos
del consumidor o hábitos de transportación).
Muchas encuestas combinan preguntas de ambos tipos. Los participantes
pueden ser preguntados si han oído ó leído sobre algún asunto… qué saben sobre él…
su opinión… con cuanta firmeza sienten y por qué… su experiencia sobre el
asunto… y ciertos datos personales que ayudará al analista a clasificar sus
respuestas (tal como edad, género, estado civil, ocupación y lugar de residencia).
Las preguntas pueden ser abiertas ("¿Por qué siente así?"), o
cerradas ("¿Aprueba usted o desaprueba?"). Los entrevistadores pueden
solicitar al participante que evalúe un candidato político o un producto usando
alguna escala, o pueden solicitarle que ordene varias alternativas.
Algunas encuestas enfocan sobre opiniones otras sobre hechos.
La forma en que se hace una pregunta puede afectar mucho los resultados de
una encuesta. Por ejemplo, una reciente encuesta de NBC/Wall Street Journal
hizo dos preguntas muy similares obteniendo resultados muy diferentes: (1)
"¿Favorece recortar programas tales como el seguro social, medicare, medicaid y subsidios a
agricultores con el fin de reducir el déficit presupuestario?" Los
resultados: a favor 23%, opuestos 66%, no opinaron 11%. (2) ¿Favorece recortar
las autorizaciones fiscales del gobierno para reducir el déficit
presupuestario? Los resultados: a favor 61%, opuestos 25%, no opinaron 14%. El
cuestionario puede ser muy breve -unas pocas preguntas, tomando cinco minutos o
menos - o puede ser bastante extenso - requiriendo una hora o más de tiempo al
participante. Como es ineficiente identificar y acercarse a una muestra
nacional grande para preguntar unos pocos ítemes de información, existen
encuestas colectivas que combinan los intereses de varios clientes en una sola entrevista. En estas
encuestas, a los participantes se les preguntará sobre una docena de preguntas
sobre un tema, una media docena sobre otro tema y así sucesivamente.
Como los cambios en actitudes o comportamiento no pueden establecerse
confiablemente con una sola entrevista, algunas encuestas usan un diseño
de panel, en el cual los mismos participantes son entrevistados en dos
ocasiones o más. Tales encuestas son usadas comúnmente durante una campaña
electoral o para trazar la salud de una familia o su patrón de compras durante un período de tiempo.
¿Quién trabaja en las Encuestas?
El trabajador de encuestas mas conocido por el público es el entrevistador
que llama por teléfono, el que aparece en la puerta del hogar o el que detiene
a personas en un centro comercial.
Tradicionalmente, las entrevistas para encuestas, aunque requieren
ocasionalmente largos días de trabajo en el campo, eran hechas principalmente
por personas empleadas a tiempo parcial. Por lo tanto este tipo de empleo era
particularmente adecuado para personas que no deseaban empleo a tiempo completo
o que querían suplementar su ingreso regular.
Cambios en el mercado de trabajo y en el nivel de automatización de las encuestas han comenzado a
alterar este patrón -aumentando el número de encuestadores que buscan trabajar
a tiempo completo. La experiencia no es usualmente requerida para un empleo de
entrevistador, aunque las destrezas básicas en el uso de computadoras adquieren cada día más importancia.
La mayoría de las organizaciones que hacen investigación proveen su
propio adiestramiento para la labor del entrevistador. Los
requisitos principales para entrevistar están la habilidad para acercarse a
personas extrañas (en persona o por teléfono), para El trabajador
de encuestas mejor conocido por el público es el entrevistador pero hay muchos
otros.
Persuadirles a participar y para recoger los datos necesarios siguiendo las
instrucciones al pie de la letra.
Menos visible, pero de igual importancia es el personal de la oficina,
quienes -entre otras cosas- planifican la encuesta, seleccionan la muestra,
supervisan las entrevistas, procesan los datos recogidos, analizan los datos e
informan los hallazgos de la encuesta.
En la mayoría de las organizaciones de investigación por encuestas, el
personal gerencial habrá tomado cursos graduados de métodos de encuestas y
poseen grados universitarios avanzados en estadísticas, sociología, sicología, mercadeo, alguna materia afín ó poseerán experiencia equivalente.
Los supervisores de nivel intermedio y los asociados de investigación
frecuentemente tendrán trasfondos académicos similares a los gerentes o habrán
avanzado desde las filas de los entrevistadores, oficinistas o codificadores
sobre la base de su competencia y experiencia.
¿Qué sobre la confidencialidad e integridad?
La confidencialidad de los datos suministrados por los participantes es una
preocupación primordial de todas las organizaciones respetables que hacen
encuestas. En el Negociado del Censo de los Estados Unidos, por ejemplo, los
datos recogidos están protegidos por ley (Título 13 del Código Legal de Estados Unidos). En Canadá, la Ley de
Estadísticas garantiza la confidencialidad de los datos recogidos por
Statistics Canadá, y otros países tiene salvaguardas similares.
Varias organizaciones profesionales que tienen que ver con métodos de
encuestas tienen un código de ética (como la Asociación Estadística Americana) que
establecen reglas para mantener la confidencialidad de las respuestas en
encuestas. La política recomendada para que las organizaciones de encuestas
salvaguarden la confidencialidad incluye:
·
Usar códigos numéricos para vincular al participante con su cuestionario y
guardar la
información sobre el vínculo nombre-código en un lugar aparte.
·
Negarse a proveer los nombres y direcciones de los participantes en la
encuesta a cualquier persona fuera de la organización de encuestas, incluyendo
a sus clientes.
·
Destruir cuestionarios e información que pueda servir para identificar los
participantes
luego que sus respuestas se hayan entrado a la computadora.
·
Omitir los nombres y direcciones de los participantes en la encuesta de
los archivos de computadora usados para análisis.
·
Presentar tabulaciones estadísticas usando categorías amplias para que los
participantes individuales no puedan ser identificados.
La confidencialidad de los datos suministrados por los participantes es una
preocupación primordial de todas las organizaciones de encuesta respetables.
¿Cuáles son nuestras preocupaciones potenciales?
La calidad de una encuesta es determinada en gran medida por su propósito y
por la forma en que es conducida.
La mayoría de las indagaciones de televisión (por ejemplo, las
"encuestas" usando el número telefónico 900) o las
"encuestas" en revista son altamente sospechosas. Estas y otras
encuestas de opinión autoseleccionadas ("self-selected opinion polls:
SLOPS)" pueden llevar a conclusiones erróneas ya que los participantes
no han sido seleccionados científicamente.
Las encuestas deben llevarse a cabo únicamente para obtener información
estadística sobre algún tema. No deben ser diseñadas para producir resultados
predeterminados o como un artificio para mercadeo o para actividades similares.
Cualquier persona a quien se le solicite que responda a una encuesta de opinión
o que se preocupe por los resultados debe primero decidir si las preguntas que
se hacen son justas.
Otra violación importante de la integridad ocurre cuando lo que parece ser una
encuesta es efectivamente un vehículo para estimular donaciones a alguna causa
o para crear una lista de direcciones para mercadear productos.
Los cuestionarios proporcionan una alternativa muy útil para la entrevista;
si embargo, existen ciertas características que pueden ser apropiada en algunas
situaciones e inapropiadas en otra. Al igual que la entrevistas, deben
diseñarse cuidadosamente para una máxima efectividad.
Recabación de datos mediante cuestionarios
Para los analistas los cuestionarios pueden ser la única forma posible de
relacionarse con un gran número de personas para conocer varios aspectos del
sistema. Cuando se llevan a cabo largos estudios en varios departamento, se
puede distribuir los cuestionarios a todas las personas apropiadas para recabar
hechos en relación al sistema. En mayor parte de los casos, el analista no verá
a los que responde; no obstante, también esto es una ventaja porque aplican
muchas entrevista ayuda a asegurar que el interpelado cuenta con mayor
anonimato y puedan darse respuestas mas honesta ( y menos respuestas prehechas
o estereotipadas). También las preguntas estandarizadas pueden proporcionar
datos más confiable.
Selección de formas para cuestionarios
El desarrollo y distribución de los cuestionarios; por lo tanto,
el tiempo invertido en esto debe utilizarse en una forma inteligente. También
es importante el formato y contenido de las preguntas en la recopilación de
hechos significativos.
Existen dos formas de cuestionarios para recabar datos: cuestionarios
abiertos y cerrados, y se aplican dependiendo de si los analistas conocen de
antemano todas las posibles respuestas de las preguntas y pueden incluirlas.
Con frecuencia se utilizan ambas formas en los estudios de sistemas.
Cuestionario Abierto
Al igual que las entrevistas, los cuestionarios pueden ser abiertos y se
aplican cuando se quieren conocer los sentimientos, opiniones y experiencias
generales; también son útiles al explorar el problema básico, por ejemplo, un
analista que utiliza cuestionarios para estudiar los métodos de verificación
de crédito, es un medio.
El formato abierto proporciona una amplia oportunidad para quienes
respondan escriba las razones de sus ideas. Algunas personas sin embargo,
encuentran más fácil escoger una de un conjunto de respuestas preparadas que
pensar por sí mismas.
Cuestionario Cerrado
El cuestionario cerrado limita las respuestas posibles del interrogado. Por
medio de un cuidadoso estilo en la pregunta, el analista puede controlar el
marco de referencia. Este formato es el método para obtener información sobre
los hechos. También fuerza a los individuos para que tomen una posición y
forma su opinión sobre los aspectos importantes.
La OBSERVACIÓN
Otra técnica útil para el analista en su progreso de investigación,
consiste en observar a las personas cuando efectúan su trabajo. Como técnica de
investigación, la observación tiene amplia aceptación científica. Los
sociólogos, sicólogos e ingenieros industriales utilizan extensamente ésta
técnica con el fin de estudiar a las personas en sus actividades de grupo y como miembros de la organización. El propósito de la organización es
múltiple: permite al analista determinar que se está haciendo, como se está
haciendo, quien lo hace, cuando se lleva a cabo, cuanto tiempo toma, dónde se
hace y por que se hace.
"¡Ver es creer! Observar las operaciones la proporciona el analista hechos
que no podría obtener de otra forma.
Tipos de Observación
El analista de sistemas puede observar de tres maneras básicas. Primero,
puede observar a una persona o actitud sin que el observado se dé cuenta y su interacción por aparte del propio analista.
Quizá esta alternativa tenga poca importancia para el análisis de sistemas,
puesto que resulta casi imposible reunir las condiciones necesarias. Segundo,
el analista puede observar una operación sin intervenir para nada, pero estando
la persona observada enteramente consciente de la observación. Por último,
puede observar y a la vez estar en contacto con las personas observas. La
interacción puede consistir simplemente en preguntar respecto a una tarea
específica, pedir una explicación, etc.
Preparación para la observación
1. Determinar y definir
aquella que va a observarse.
2. Estimular el tiempo
necesario de observación.
3. Obtener la autorización
de la gerencia para llevar a cabo la observación.
4. Explicar a las personas
que van a ser observadas lo que se va a hacer y las razones para ello.
Conducción de la observación
1.
Familiarizarse con los componentes físicos del área inmediata de
observación.
2.
Mientras se observa, medir el tiempo en forma periódica.
3.
Anotar lo que se observa lo más específicamente posible, evitando las
generalidades y las descripciones vagas.
4.
Si se está en contacto con las personas observadas, es necesario abstenerse
de hacer comentarios cualitativos o que impliquen un juicio de valores.
5.
Observar las reglas de cortesía y seguridad.
Secuela de la observación
1.
Documentar y organizar formalmente las notas, impresionistas, etc.
2.
Revisar los resultados y conclusiones junto con la persona observada, el
supervisar inmediato y posiblemente otro de sistemas.
Es una representación pictórica de los pasos en proceso. Útil para
determinar cómo funciona realmente el proceso para producir un resultado. El
resultado puede ser un producto, un servicio, información o una combinación de
los tres. Al examinar cómo los diferentes pasos es un proceso se relacionan
entre sí, se puede descubrir con frecuencia las fuentes de problemas potenciales. Losdiagramas de flujo se pueden aplicar a
cualquier aspecto del proceso desde el flujo de materiales hasta los pasos para hacer la venta u ofrecer un producto. Con frecuencia este nivel
de detalle no es necesario, pero cuando se necesita, el equipo completo de
trabajo más pequeños pueden agregar niveles según sea necesario durante
el proyecto.
Cuando un equipo necesita ver cómo funciona realmente un proceso completo.
Este esfuerzo con frecuencia revela problemas potenciales tales como cuellos de
botella en el sistema, pasos innecesarios y círculos de duplicación de trabajo.
Algunos aplicaciones comunes son:
·
Identificar oportunidades de cambios en el proceso.
·
Identificar organizaciones que deben estar representadas en el equipo.
·
Desarrollar una base común de conocimiento para los nuevos miembros del
equipo.
·
Involucrar a trabajadores en los esfuerzos de resolución de problemas para
reducir las resistencias futura al cambio.
Identificación de las causas principales:
·
Desarrollar planes para reunir datos.
·
Discutir las formas de estratificar los datos para el análisis para
identificar las causas principales.
·
Examinar el tiempo requerido para las diferentes vías del proceso.
Diseño de soluciones
·
Describir los cambios potenciales en el proceso y sus efectos potenciales.
·
Identificar las organizaciones que será afectadas por los cambios
propuesto.
·
Explicar otros el proceso actual y la solución propuesta.
·
Superar la resistencia al cambio demostrando cómo los cambios propuestos
simplificarán el proceso.
Control (retener las Ganancias):
·
Revisar y establecer controles y monotorías al proceso.
·
Auditar el proceso periódicamente para asegurar que están siguiendo los
nuevos procedimientos.
·
Entrenar a nuevos empleados.
¿Cómo se Utiliza?
1. PROPÓSITO: analizar como
se pretende utilizar el Diagrama de Flujo. Exhibir esta hoja en el pared y
consultarla en cualquier momento para verificar que se Diagrama de Flujo es
apropiado para las aplicaciones que se pretende.
2. DETERMINAR EL NIVEL DE
DETALLE REQUERIDO.
3. DEFINIR LOS LIMITES:
después de establecer los límites del proceso, enumerar los resultados y los
clientes en el extremo derecho del diagrama.
4. UTILIZAR SÍMBOLOS APROPIADOS: utilizando los símbolos
apropiados para el Diagrama de Flujo, presentar las respuestas como los
primeros pasos en el diagrama.
5. HACER PREGUNTAS: para
cada input, haga preguntas como:
·
¿Quién recibe el input?
·
¿Qué es lo primero que se hace con el input?
1.
DOCUMENTAR: cada paso en la secuencia, empezando con el primer (ó último)
paso. Para cada paso, hacer preguntas como:
·
¿Qué produce este paso?
·
¿Quién recibe este resultado?
·
¿Qué pasa después?
·
¿Alguno de los pasos requiere de inputs que actualmente no se muestran?
1.
COMPLETAR: continuar la construcción del Diagrama de Flujo hasta que se
conecte todos los resultados (outputs) definidos en el extremo derecho del
diagrama. Si se encuentra un segmento del proceso que es extraña para todos en
el salón, se deberá tomar nota y continuar haciendo el diagrama.
2.
REVISIÓN: Preguntar:
·
¿Todos los flujos de información encajan en los inputs y outputs del
proceso?
·
¿El Diagrama capta de forma exacta lo que realmente ocurrió, a diferencia
de la forma cómo se piensa que las cosas deberías pasar o como fueron diseñadas
originalmente?
1.
DETERMINAR OPORTUNIDADES
Nota: El Diagrama de flujo final deberá actuar como un registro de cómo el proceso actual realmente
opera. Indicar la fecha.
Aunque hay literalmente docenas de símbolos especializadas utilizados para
hacer Diagrama de Flujos, se utiliza con más frecuencia los siguientes:
Para ver el gráfico seleccione la opción "Descargar"
Las "líneas de flujos" son utilizadas para representar el
progreso de los pasos en la secuencia. La punta de la fecha indica la dirección del flujo del proceso.
Otros dos símbolos que no son utilizados tan comúnmente y que pueden ser
útiles son:
El "Símbolo del documento" representa la información escrita
pertinente al proceso.
El "Símbolo de la Base de Datos" representa información almacenada
electrónicamente con respecto al proceso
Consejos para la construcción / Interpretación:
Si un Diagrama de Flujo se construye de forma apropiada y refleja el
proceso de la forma que realmente opera, todos los miembros del equipo poseerán
un conocimiento común, exacto del funcionamiento del proceso. Adicionalmente,
el equipo no necesita invertir el tiempo y la energía en observar el proceso
físicamente cada vez que se quiera identificar problemas para trabajar,
discutir teorías sobre las causas principales, examinar el impacto de las
soluciones propuestas o discutir las formas para mantener las mejoras.
Los Diagramas de Flujo pueden ayudar a un equipo en su tarea de diagnóstico para lograr mejoras. Uno de sus usos
es el de ayudar a un equipo a generar teorías sobre las posibles causas
principales de un problema. El Diagrama de Flujo se dibuja en una pared de la
sala de reuniones. El equipo que investiga un problema redacta una descripción del problema en un pedazo pequeño
del papel y lo pega en el Diagramas de Flujo en el punto, en el proceso donde el
problema se ha detectado. El equipo luego discute cada uno de los pasos en el
proceso antes del punto donde el problema se ha detectado, y produce teorías
sobre las cosas que podrían salir mal en el paso del proceso de forma
sistemática a medida que producen teorías sobre las posibles causas principales
del problema.
Otro uso de un Diagramas de Flujo es el de ayudar a un equipo a identificar
las formas apropiadas para separar los datos para su análisis. Por ejemplo,
considérese el problema de analizar los tiempos de reparación. Una rápida
revisión del Diagramas de Flujo puede sugerir un número de grupos posibles que
pueden explicar el tiempo que se necesita para hacer reparación.
Relación con otras herramientas:
·
Mapa de Relaciones
·
Mapa de Proceso Interfuncional (Cross-Funcional)
Los diccionarios de datos son el segundo componente
del análisis del flujo de datos. En sí mismos los diagramas de flujo de datos
no describen por completo el objeto de la investigación. El diccionario de
datos proporciona información adicional sobre el sistema. Esta sección analiza
que es un diccionario de datos, por qué se necesita en el análisis de
flujo de datos y como desarrollarlo. Se utilizará el ejemplo del sistema
de contabilidad para describir los diccionarios de
datos.
Un diccionario de datos es una lista de todos los elementos incluido en el
conjunto de los diagramas de flujo de datos que describen un sistema. Los
elementos principales en un sistema, estudiados en las secciones anteriores,
son el flujo de datos, el almacenamiento de datos y los procesos. El
diccionario de datos almacena detalles y descripciones de estos elementos.
Si los analistas desean conocer cuántos caracteres hay en un dato, con qué
otros nombres se le conoce en el sistema, o en donde se utilizan dentro del
sistema deben ser capaces de encontrar las respuesta en un diccionario de datos
desarrollado apropiadamente.
El diccionario de dato se desarrolla durante el análisis de flujo de datos
y ayuda el analista involucrado en la determinación de los requerimientos de
sistemas. Sin embargo, como se verá más adelante, también el contenido del
diccionario de datos se utiliza durante el diseño del sistema.
En informática, base de datos acerca de la terminología
que se utilizará en un sistema de información. Para comprender mejor el
significado de un diccionario de datos, puede considerarse su contenido como
"datos acerca de los datos"; es decir, descripciones de todos los
demás objetos (archivos, programas, informes, sinónimos...) existentes en el
sistema. Un diccionario de datos almacena la totalidad de los diversos esquemas
y especificaciones de archivos, así como sus ubicaciones. Si es completo
incluye también información acerca de qué programas utilizan qué datos, y qué
usuarios están interesados en unos u otros informes. Por lo general, el
diccionario de datos está integrado en el sistema de información que describe.
Descripción de los Datos en el Diccionario
Cada entrada en el diccionario de dato consiste en un conjunto de detalles
que describen los datos utilizados o producidos en el sistema. Cada articulo se
identifica por un nombre de dato, descripción, sinónimo y longitud de campo y tiene
valores específicos que se permiten para éste en el sistema estudiado.
Nombre de los Datos
Para distinguir un dato de otro, los analista les asigna nombre
significativos que se utilizan para tener una referencia de cada elemento a
través del proceso total de desarrollo de sistemas. Por lo tanto, debe tenerse
cuidado para seleccionar, en forma significativa y entendible, los nombres de
los datos, por ejemplo la fecha de factura es más significativa si se llama FECHA FACTURA
que si se le conoce como ABCXXX.
Descripción de los Datos
Establece brevemente lo que representa el dato en el sistema; por ejemplo,
la descripción para FECHA-DE-FACTURA indica que es la fecha en la cual se está
preparando la misma (para distinguirla de la fecha en la que se envió por
correo o se recibió.
Las descripciones de datos se deben escribir suponiendo que a gente que los
lea no conoce nada en relación del sistema. Deben evitarse termino especiales o
argot, todas las palabras deben se entendible para el lector
Alias
Con frecuencia el mismo dato puede conocerse con diferentes nombres,
dependiendo de quien lo utilice. El uso de los alias deben evitar confusión. Un
diccionario de dato significativo incluirá todos los alias.
Longitud de campo
Cuando las característica del diseño del sistema se ejecuten más tarde en
el proceso de desarrollo del sistemas, será importante conocer la cantidad de
espacio que necesita para cada dato.
Valores de los datos
En algunos proceso solo se permiten valores de datos específicos. Por
ejemplo, en muchas compañías con frecuencia los números de orden de compra se
proporcionan con un prefijo de una letra para indicar el departamento del
origen.
Registro de las descripciones de datos
Dadas que las descripciones se utilizarán en forma repetitiva a través de
una información y después, durante el diseño, se sugiere un formato fácil para
utilizar que simplifique el registro y los detalles de consulta cuando se
necesiten.
La Recolección de Datos, consiste en la recopilación de información; se
lleva a cabo por medio
de entrevistas, cuestionarios y observación; donde el analista obtiene y
desarrolla los sistemas de información logrando sus metas y objetivos.
El analista debe de demostrar y desarrollar las destrezas de sus
conocimientos manifestando su honestidad, imparcialidad, habilidad,
objetividad, control, comunicación, comprensión y cortesía para lograr la
búsqueda de información a través de las herramientas antes mencionada.
La entrevista, se lleva a cabo en todos los niveles de operación desde el
Presidente o el Jefe de Operaciones.
Utilizando procedimientos que pueden varar desde muy formales hasta los
casuales.
El cuestionario, es otra de las utensilios que usa el analista con el fin
de lograr un consenso, siendo un canal de comunicación poco limitado, el
analista debe determinar lo que desea saber, estructurar preguntas que pueden
dar las respuestas y formular el cuestionario.
La observación, se emplea para verificar los resultados de una entrevista y
tiene una aceptación científica.
El diagrama de flujo, es el proceso para plantear un problema y determinar
un resultado en una empresa.
El diccionario de datos, se aplica para la examinación de los diagramas de
flujos de datos y a su vez registra detalles adicionales dentro del flujo de un
sistema.
20 03 2016
Invitación: ingresa al enlace para inscribirte:
http://www.superate.gov.co/
08 03 2016
Enlaces para las estrategias de apoyo.
Ejercicios con números
reales
Semejanza de triángulos
Enlace mediafire números complejos
Esto le servirá para preparar la evaluación de recuperación.
Descargar desde el enlace, el resumen de semejanza de triángulos. luego de leer realizar las autoevaluaciones.
Hacer clic en :
Para las autoevaluaciones:
Ejercicios interactivos de semejanza de triángulos
semejanza de triang
criterios de semejanza
http://www.vitutor.com/geo/eso/ss_5e.html
10 03 2016
10 03 2016
Logro: Repasa operaciones básicas en el
campo de los números reales con aplicaciones cotidianas.
1. Un comerciante compró una pieza
de tela de 23 metros por $ 195.000 . Después vendió cada metro a $ 18.750.
¿Cuánto gana el comerciante en la venta de cada metro?
2. Adrían compró una moto por
un valor de $ 9.480.000. Primero
pagó la mitad del valor y el resto en 12
mensualidades iguales. ¿Cuánto pagó en cada mensualidad?
3. Alicia ha vendido hoy 24 sillas
iguales. Un armario y un sillón por un
valor de 3.200.000. El armario costó $ 1.750.000 y el sillón $850.000. ¿Cuánto
costó cada silla?
4.
Un ciempiés tiene 42 patas. Este levanta 3/7 de sus
patas. Cuántas patas levanta?
5.
En una granja hay 150 animales. 2/6 son vacas, 1/5 son
gallinas, 3/10 cerdos, el resto son patos. ¿Cuantos animales de cada clase hay?
6. Un rollo de tela mide 36.25
metros de largo y tiene 2.30 metros de ancho. ¿Cuántos tozos cuadrados de 1.15 metros se pueden
obtener de él?
7 En Diciembre compré unos tenis
de $ 85.000 con un descuento del 15%; una camiseta de $28.000 con un descuento
del 10%; y unos pantalones de $62.000 con descuento del 20%. Si llevaba $
200.000. a) ¿Cuánto dinero me sobró? b) ¿
Cuánto fue el descuento total? C)
¿Cuánto me ahorré en los tenis? D) ¿De cuánto habría sido el importe sin los
descuentos?
Operaciones con números
complejos
11 11 2016
Enlaces para presentar el quiz de
Enlaces para descargar o ver los talleres de estrategias de apoyo 2015
9º álgebra
Enlace para descargar el taller de apoyo del IV periodo:
http://www.mediafire.com/view/0goakll890uueod/taller_apoyo_9_IV_per_2015.pdf
Este taller vale 50% y el quiz virtual 50%
Este taller vale 50% y el quiz virtual 50%
Autoevaluación del estudiente IV periodo:
Autoevaluación del estudiante:
Autoevaluación IV periodo
|
07 10 20
Enlaces para repasar Progresiones geométricas:
Ayudas en videos:
Progresiones Geométricas -
Ejercicio 1
Progresiones Geométricas -
Ejercicio 2
Progresiones Geométricas -
Ejercicio 3
Puedes practicar P.A. y preparar la evaluación ,realizando las siguientes autoevaluaciones:
inténtalo:
inténtalo:
inténtalo:
inténtalo:
inténtalo:
12 09 2015
Progresiones aritméticas (P.A.), resumen de clase:
Videos de ayuda P.A.:
Progresiones Aritméticas -
Ejercicio 1
Progresiones Aritméticas -
Ejercicio 2
Progresiones Aritméticas -
Ejercicio 4
Progresiones Aritméticas -
Ejercicio 5
Progresiones Aritméticas -
Ejercicio 4
Quiz virtual ecuaciones logarítmicas
Ecuaciones logarítmicas resumen de clase:
Una ecuación
logarítmica es aquella en la que la incógnita aparece en una expresión
afectada por un logaritmo.
Así en la ecuación 2 log x = 1 + log (x - 0,9), en la que
la incógnita x aparece tras el signo
de logaritmo, es logarítmica.
Un sistema de ecuaciones logarítmicas es
un sistema formado por ecuaciones logarítmicas.
Cómo se resuelven ecuaciones logarítmicas
Para resolver estas ecuaciones se
intenta, aplicando las propiedades de los logaritmos, llegar a expresiones del
tipo log A = log B.
Una vez conseguido, se aplica la
equivalencia
log A
= log B Û A = B,
deduciendo, a partir de aquí, los
valores de las incógnitas.
| En algunas ecuaciones logarítmicas se
deben aplicar las propiedades de la logaritmación para hallar la solución |
Log 3[(x+4)(x-4)] = 2 Log2(x2)2-Log2(-x)2=4
Log 3(x2-16) = 2 Log 2x4 - Log 2x2 = 4
x2-16 = 32 Log 2(x4 /x2)=4
x2 = 9 + 16 x2 = 24
x2 = 25 x2 = 16
x = ± 5 x = ± 4
En la primer ecuación, solo se verifica la solución positiva: x=5, mientras que en la segunda solo la negativa: x=-4
| En otras ecuaciones logarítmicas es
necesario realizar un cambio de variable. |
z = Log2x
Nueva ecuación a resolver: z2-5z+4=0,
de la cual resulta z1=4 y z2=1. Utilizando el cambio de
variable, tenemos las siguientes ecuaciones: Log2x =
4 y Log2x=1,
de las que obtenemos, aplicando la definición de logaritmos: x1=16 y
x2=2.
Videos de ayuda :
Ecuaciones Logarítmicas
https://www.youtube.com/watch?v=gSlkeCgTSuk
Ecuaciones Logarítmicas - Ejercicio 1
https://www.youtube.com/watch?v=riqZcExsvcE
Ecuaciones Logarítmicas - Ejercicio 2
https://www.youtube.com/watch?v=1qVTH0Dr4C0
Ecuaciones Logarítmicas - Ejercicio 3
https://www.youtube.com/watch?v=UcgsO70f5sU
Ecuaciones Logarítmicas - Ejercicio 4
https://www.youtube.com/watch?v=LW_sP5jDBQA
Ecuaciones Logarítmicas - Ejercicio 5
https://www.youtube.com/watch?v=g3KhxSJVcSg
Ecuaciones Logarítmicas - Ejercicio 6
https://www.youtube.com/watch?v=EaxI046b7t8
Ecuaciones Logarítmicas - Ejercicio 7
https://www.youtube.com/watch?v=ZF47GJUB6iU
Ecuaciones Logarítmicas - Ejercicio 8
https://www.youtube.com/watch?v=5KWcFn1jWDs
Ecuaciones Logarítmicas - Ejercicio 9
https://www.youtube.com/watch?v=_dDp9BoFODI
Ecuaciones Logarítmicas - Ejercicio 10
https://www.youtube.com/watch?v=yLoA7aEGJz0
Ecuaciones Logarítmicas - Ejercicio 11
https://www.youtube.com/watch?v=dm8d4yUTqJ0
Ecuaciones Logarítmicas - Ejercicio 12
Ecuaciones Logarítmicas - Ejercicio 13
https://www.youtube.com/watch?v=f1_ACPdtA-Q
Ecuaciones Logarítmicas - Ejercicio 14
https://www.youtube.com/watch?v=dApslxUJMhUAutoevaluación del estudiante:
Autoevaluación III periodo
|
21 08 20
Enlaces para el
Resumen de logaritmos y sus propiedades(videos):
Logaritmos 01 matemáticas
Logaritmos 02 matemáticas
Logaritmos 03 matemáticas
Logaritmos 04 matemáticas
08 08 2015
04 07 2015
Recomendaciones para resolver problemas
100 problemas de matemáticas que todo estudiante de bachillerato debe saber y conocer.
Descargar de:
clic en DOWNLOAD NOW
http://www32.zippyshare.com/v/s2eO3ER0/file.html
enlace activo 30 días 03 05 20
28 04 20
Enlaces que les pueden servir para comprobar gráficas de funciones on line:
Graficador de
funciones en linea:
5 graficadores on line
| Z |
Resumen de relaciones y funciones
Relaciones y
funciones
Entender los conceptos de Relación y de Función es de suma importancia en
Matemática.
Para lograr esa comprensión es necesario adentrarnos en la noción de Correspondencia,
ya que esta tiene un papel fundamental en las relaciones y funciones.
Lo primero es entender que Correspondencia es equivalente a
Relación. En nuestra lengua, decir “en relación a”, es equivalente a decir
“corresponde a”.
Ejemplos:
En una tienda comercial, cada artículo está relacionado con
su precio; o sea, a cada artículo le corresponde un precio.
En la guía telefónica, cada cliente está relacionado con
un número; o sea, a cada nombre de la guía le corresponde un
número.
Definición matemática de Relación y
de Función
En matemática, Relación es la correspondencia de un primer
conjunto, llamado Dominio, con un segundo conjunto, llamado Recorrido,
contradominio o Rango, de manera que
a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o
Rango.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
De las definiciones anteriores podemos deducir que todas las funciones son relaciones,
pero no todas las relaciones son funciones.
También debemos agregar que toda ecuación es una Relación, pero
no toda ecuación es una Función.
Todas las Relaciones pueden ser graficadas en el Plano
Cartesiano.
Ver: Plano Cartesiano
Dados dos conjuntos A y B una relación definida de A en B es un conjunto de
parejas ordenadas (par ordenado) que hacen verdadera una proposición;
dicho de otro modo, una relación es cualquier subconjunto del producto
cartesiano A x B
Ejemplo 1.
Si A = {2, 3} y B = {1, 4, 5}, encontrar tres relaciones definidas de
A en B.
Solución
El producto cartesiano de A x B está conformado por las siguientes parejas
o pares ordenados:
A x B = {(2, 1), (2, 4), (2, 5), (3, 1), (3, 4), (3, 5)}
Y cada uno de los siguientes conjuntos corresponde a relaciones definidas
de A en B:
R1 = {(2, 1), (3, 1)}
R2 = {(2, 4), (2, 5), (3, 4), (3, 5)}
R3 = {(2, 4), (3, 5)}
La relación R1 se puede definir como el conjunto de pares cuyo segundo
elemento es 1, esto es, R1 = {(x, y) / y =
1}.
La relación R2 está formada por los pares cuyo primer componente es menor
que el segundo componente, R2 = {(x, y) / x < y}
Y la relación R3 está conformada por todos los pares que cumplen con que el
segundo componente es dos unidades mayor que el primer componente, dicho de
otro modo, R3 = {(x, y) / y = x + 2}
Así, se puede continuar enumerando relaciones definidas a partir de A x B.
Como se puede ver, la regla que define la relación se puede escribir mediante ecuaciones o desigualdades que relacionan los valores
de x e y. Estas reglas son un medio conveniente
para ordenar en pares los elementos de los dos conjuntos.
Ejemplo 2.
Dados los conjuntos C = {1, –3} y D = {2, 3, 6}, encontrar todos los pares
ordenados (x, y) que satisfagan la relación
R = {(x, y) / x + y =
3}
Solución
El producto cartesiano de C x D está formado por los siguientes pares
ordenados
C x D = {(1, 2),
(1, 3), (1, 6), (–3, 2), (–3, 3), (–3, 6)}
Las parejas ordenadas que satisfacen que la suma de sus componentes sea
igual a 3 son:
R
= {(1, 2), (–3, 6)}
Toda relación queda definida si se conoce el conjunto de partida, el
conjunto de llegada y la regla mediante la cual se asocian los elementos. En el
ejemplo anterior, el conjunto de partida corresponde al conjunto C,
el conjunto de llegada es el conjunto D y la expresión x + y =
3 es la regla que asocia los elementos de los dos conjuntos.
Dominio y rango de una
relación
El dominio de una relación es el conjunto de preimágenes; es
decir, el conjunto formado por los elementos del conjunto de partida que están
relacionados. Al conjunto de imágenes, esto es, elementos del
conjunto de llegada que están relacionados, se le denomina recorrido o
rango.
Ejemplo 3
Sea A = {1, 2, 3, 4} y B = {4, 5, 6, 7, 8} y R la relación definida
de A en B determinada por la regla “y es el doble de x”
o “y = 2x”, encontrar dominio y rango de la relación.
Solución
El total de pares ordenados que podemos formar, o producto cartesiano es:
A x B = {(1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (2, 4), (2, 5), (2,
6), (2, 7), (2, 8), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (4, 4), (4, 5), (4,
6), (4, 7), (4, 8)}
Pero los pares que pertenecen a la relación R (y = 2x) son solo:
R = {(2, 4), (3, 6), (4, 8)}
En esta relación vemos que: “4 es el doble de 2”; esto es, “4 es la imagen
de 2 bajo R”, dicho de otro modo, “2 es preimagen de 4”.
Así, el dominio y rango son:
D = {2, 3, 4}
Rg = {4, 6, 8}
Según lo que vemos, ¿Qué relación hay entre el Dominio y el conjunto de
partida?
En el Dominio falta el elemento 1 del conjunto de partida, por lo tanto el
Dominio es un subconjunto de A.
Otra pregunta: ¿Todo elemento del conjunto de llegada es elemento del
rango?
La respuesta es no, pues en el rango faltan el 5 y el 7.
Representación gráfica
de las relaciones
Los pares ordenados se pueden representar gráficamente por medio de diagramas
sagitales o por medio de puntos en el plano cartesiano.
Veamos el siguiente ejemplo.
Ejemplo 4
Si A = {1, 2, 3, 4, 5} y B = {1, 3, 5, 7, 9} y R la relación
definida por la regla
R = {(x, y) / y = 2x + 1},
graficar R.
Solución
Los pares ordenados que pertenecen a la relación (que cumplen con y =
2x + 1) son:
R
= {(1, 3), (2, 5), (3, 7), (4, 9)}
Fuente Internet:
Es propiedad: www.profesorenlinea.cl - Registro N° 188.540
Tipos de relaciones y
funciones 1
Amplia tus conceptos de funciones
Ejercicios interactivos para que te autovalues:
coordenadas
representación de puntos
tablas de valores
representación grafica
características
funcion
función lineal
función afin
función constante
para ampliar mas
graficas de funciones
18 04 20
Técnica de respiración
La
inhalación (succión de aire) se debe hacer, para efectos de relajación,
únicamente con la nariz y la exhalación (expulsión de aire) por la boca. Al
cerrar los ojos uno puede identificar con mayor facilidad el recorrido del aire
por el cuerpo. Se recomienda, que la técnica de respiración se practique con
las manos sobre la cavidad abdominal para corroborar el movimiento del
diafragma.
Complementando
el ejercicio anterior, se recomienda optimizar la relajación a través de estiramientos
musculares tales como:
-
Movimiento del cuello (vertical-horizontal- circular).
-
Estiramiento de brazos y antebrazos.
6
-
Estiramiento de espalda hacia abajo y atrás.
-‐ Estiramiento de Torso
Adicional
a la relajación, se utilizan ejercicios mentales que consisten en formar una representación
imaginaria de la situación que genera estrés durante 30-40 segundos, sustituyendo
los peores escenarios con los realistas, que aluden a la seguridad de lo que se
sabe.
3.2.2
Consideraciones
Algunas
recomendaciones importantes para el control de la ansiedad se concentran en
tres momentos: un día antes del examen, momentos antes de que ocurra y durante
éste.
Un día
antes:
• Evitar
estudiar lo que se cree que no se ha aprendido aún. Esto genera una fatiga y/o bloqueo
mental.
•
Realizar las actividades habituales del día y en la medida de lo posible,
realizar ejercicio físico moderado (que bien pueden ser ejercicios de
relajación).
• Evitar
desvelarse. Dormir permite la recuperación física, mental y emocional.
• Cenar
ligero. Una alimentación con alta cantidad de carbohidratos y grasas puede
causar malestar en caso de que se presente un cuadro de estrés o ansiedad.
Momentos
antes:
• No
hablar del examen, las posibilidades de su contenido, inseguridades o seguridad
en lo que se sabe.
Identificar
a los estudiantes que presentan ansiedad para apartarlos un momento del resto y
practicar ejercicios de relajación.
Durante:
• Ante el
bloqueo mental: respirar un minuto, leer y comprender la pregunta antes de responder.
Lo
anterior no pretende englobar la totalidad de técnicas y recomendaciones útiles
para la presentación de pruebas por computador, de modo que además de llevarlas
a cabo con los estudiantes, es recomendable buscar otras técnicas útiles que
puedan apoyar su preparación.
Autoevaluación del estudiante:
|
El código Dane de Sorjuana es:
29 02 2015
Enlaces para practicar racionalización:
Racionalización
Ejercicios interactivos:
28 02 2015
Enlaces para el quiz diagnóstico de finanzas personales:
9.1:
9.2:
Presentación y socialización del blog de finanzas para el cambio adscrito al proyecto institucional,cátedra de emprendimiento:
https://finansor.wordpress.com/
22 02 2015
Enlaces para practicar potenciación:
ejercicios interactivos:
Página para practicar jugando.
Me la juego por saber:
El código Dane de Sorjuana es:
105001001848
15 02 2015
Taller completo para estudiar radicación:
ejercicios
14 11 2014
Notas del IV periodo
Algebra
9.1
Geometría
Álgebra
9.2
Geometría
08 11 2014
Quiz P.G IV periodo clic en los enlaces:
9.1:
Quiz de geometría IV periodo
9.1:
9.2:
Enlaces:
9.1:
04 11 2014
Taller de finanzas para prueba saber.
Prueba saber 9° finanzas personales
1.
Lucía y sus amigas van a alquilar una casa. Todas llevan dos meses trabajando.
No tienen ahorros. A todas les pagan mensualmente y acaban de recibir sus
sueldos. Han preparado esta lista de “ asuntos pendientes:
A.
Contratar TV por cable
B.
Pagar el alquiler
C.
Comprar muebles de exterior
D.
Comprarse vestidos nuevos
¿ Qué tarea de la lista es probable que
requiera atención prioritaria de Lucía y sus amigas?
2.
Todos los meses a Ana le ingresan el sueldo en su cuenta bancaria. Esta es la
nómina correspondiente a l mes de Julio:
Nómina del empleado: Ana Cano.
Puesto: Jefe de sección….del 1° del 31 de
julio.
Sueldo bruto…… 2800 $
Deducciones….. 300 $
Sueldo neto….. 2500 $
Sueldo bruto anual acumulado…………. 19600 $
El dinero que ingresó la empresa a la
cuneta de Ana el 31 de Julio fue de:
A.
3266
B.
2800
C.
1800
D.
2500
3.
Natalia trabaja en un restaurante 3 tardes a la
semana. Cada tarde, trabaja 4 horas y gana 10 US por
hora. Cada semana, gana además 80 US en
propinas. Natalia ahorra exactamente la mitad de la cantidad total de dinero
que gana cada semana.
Natalia quiere ahorrar 600 US para ir de
vacaciones. ¿Cuántas semanas tardará Natalia en ahorrar 600 US?
A.
6
B.
10
C.
3
D.
12
4.
David tiene cuenta en el banco Zedland. Recibe
este mensaje de correo “ Estimado cliente del banco, se ha producido un fallo
en el servidor del banco Zedland y sus datos de acceso por internet se han
borrado . En consecuencia no dispone usted de acceso a la banca por internet.
Lo que es más importante, su cuenta ha dejado de ser segura. Le rogamos hacer
clic en el enlace de abajo y siga las instrucciones para restablecer el
acceso. Le vamos a pedir que introduzca sus datos de banca por internet.
¿Cuál sería un mejor consejo para David? :
A.
Responder al mensaje y dar los datos de banca por in ternet
B.
Responder al mensaje y pedir más información.
C.
Contactar con su banco y preguntar sobre el
mensaje.
D.
Si el enlace es el mismo que la dirección web de
su banco pinchar en el enlace y seguir las instrucciones.
5.
Antonio recibe al mes $ 130 y tiene las
responsabilidades de pago:
Renta $ 50 cada mes
Agua $ 10 cada dos meses
Luz $ 8 cada mes
Gasolina $ 5 cada mes
Comida $ 20 cada mes
Ahorro programado $ 20 cada 2 meses.
El mes pasado tuvo que hacer
todos los pagos de la lista y este mes cumple años su mamá. ¿Cuánto es lo
máximo que Antonio puede gastar en el regalo de su mamá?
A.
$ 17
B.
$ 27
C.
$ 37
D.
$ 47
6.
Un país no cuenta con el dinero suficiente para
atender
Algunas de sus necesidades. Una forma en que el país podría conseguir dinero en el corto plazo es aumentar :
A.
El gasto del país en educación y salud.
B.
La compra de productos en el extranjero
C.
Una inversión destinada a edificios y carreteras
D.
El valor de los impuestos pagados por los
ciudadanos.
7.
La inflación es el aumento generalizado de los
precios de los bienes de la economía , es decir, si con $ 1000 hoy se compra un
helado, y en un mes $ 1000 Ya no alcanzan para comprarlo es porque el precio
subió, lo que significa que hay inflación . Por lo tanto la tasa de inflación
refleja el aumento porcentual de los precios en un periodo.
Cada mes Rosita hace un mercado en el mismo
supermercado y siempre comprar la misma
lista de productos que le cuesta $ 150.000
Este mes la inflación aumentó un 5%
, lo que afecta a Rosita porque al momento
de pagar el mercado.
A.
El costo total disminuyó 5%
B.
El costo total aumentó 10%
C.
Rosita pagó más para poder llevar la lista de
todos los meses.
D.
Rosita pagó lo mismo por el mercado de todos los
meses.
8.
Pedro se acaba de graduar en la universidad.
Hace un mes pasó hojas de vida para conseguir trabajo y lo contactaron de
cuatro sitios para informarle que fue seleccionado y le ofrecen esta propuestas
de las cuales debe elegir :
1.
Asistente, contrato por 16 meses con $ 1.200.000
de salario, a 10 km de su casa y 20% de
probabilidad de ser ascendido en el primer año.
2.
Asesor. Contrato a 18 meses con $ 1.400.000 a 16
km de distancia se su casa y 40% de ser ascendido en el primer año.
3.
Analista, contrato a 17 meses con $ 1.500.000 de salario y a 12 km
de su casa y 10% de probabilidad de ascenso.
4.
Consultor. Contrato a 15 meses con $ 1.300.000 , a 14 km de su
casa y 60% de ser ascendido.
Pedro debe seleccionar una de las opciones de trabajo de acuerdo con lo
más importante para él.
A partir de la información dada es correcto afirmar que:
A.
Si es su estabilidad laboral debe escoger el
cargo de analista.
B.
Si es su proyección profesional debe escoger el
cargo de consultor.
C.
Si es su nivel de ingresos debe escoger el cargo
de asistente.
D.
Si es el tiempo de transporte debe escoger el
cargo de asesor.
Análisis y soluciones al taller
Francisco recibe al mes $130 y tiene las responsabilidades de pago:
Renta: $50 cada mes.
Agua: $10 cada dos meses.
Luz: $8 cada mes.
Gasolina: $5 cada mes
Comida: $20 cada mes.
Ahorro: $20 cada dos meses.
El mes pasado tuvo que hacer todos los pagos de la lista y este mes cumple años
su mamá. ¿Cuánto es lo máximo que Francisco puede gastar en el regalo de su
mamá?
A. $17.
B. $27.
C. $37.
D. $47.
En esta pregunta el estudiante tiene en cuenta que Francisco realizó todos los
pagos el mes pasado y que hay pagos que debe realizar cada dos meses, por lo
cual no debe pagar agua ni abonar para su ahorro programado. Por lo tanto,
dispone de $30 más para comprar el regalo de cumpleaños de su mamá mientras que
en los meses que hace todos los pagos le quedan 17. Respuesta: D.
B. La compra de productos en el extranjero.
C. La inversión destinada a edificios y carreteras.
D. El valor de los impuestos pagados por los ciudadanos.
En esta pregunta el estudiante debe identificar en las opciones las que
corresponden a ingresos o egresos del país, y evidenciará que los impuestos
representan un ingreso que permite consecución de dinero a corto plazo. Por lo
tanto, su respuesta será la D.
A. El costo total disminuyó 5 %.
B. El costo total aumento 10 %.
C. Juanita pagó más para poder llevar la lista de todos los meses.
D. Juanita pagó lo mismo por el mercado de todos los meses.
2. Asesor, contrato a 18 meses. $1.400.000, a 16 km de distancia de su casa y
40 % de ser ascendido en el primer año.
3. Analista, contrato a 17 meses, $1.500.00 de salario, a 12 km de distancia y
10 % de probabilidades de ascenso.
4. Consultor, contrato a 15 meses, $1.300.000, a 14 km y 60 % de posibilidades
de ascenso.
A. Si es su estabilidad laboral debe escoger el cargo de analista.
B. Si es su proyección profesional debe escoger el cargo de consultor.
C. Si es su nivel de ingresos debe escoger el cargo de asistente.
D. Si es su tiempo de transporte debe escoger el cargo de asesor.
El estudiante identifica que la mejor proyección profesional está asociada con
la mayor probabilidad de ser ascendido en el primer año, por lo que si para
Pedro lo más importante es su proyección profesional, debe escoger el cargo de
Consultor.
me la juego por saber:
Repasar conceptos de finanzas en el enlace:
Análisis y soluciones al taller
Francisco recibe al mes $130 y tiene las responsabilidades de pago:
Renta: $50 cada mes.
Agua: $10 cada dos meses.
Luz: $8 cada mes.
Gasolina: $5 cada mes
Comida: $20 cada mes.
Ahorro: $20 cada dos meses.
El mes pasado tuvo que hacer todos los pagos de la lista y este mes cumple años su mamá. ¿Cuánto es lo máximo que Francisco puede gastar en el regalo de su mamá?
A. $17.
B. $27.
C. $37.
D. $47.
En esta pregunta el estudiante tiene en cuenta que Francisco realizó todos los pagos el mes pasado y que hay pagos que debe realizar cada dos meses, por lo cual no debe pagar agua ni abonar para su ahorro programado. Por lo tanto, dispone de $30 más para comprar el regalo de cumpleaños de su mamá mientras que en los meses que hace todos los pagos le quedan 17. Respuesta: D.
Renta: $50 cada mes.
Agua: $10 cada dos meses.
Luz: $8 cada mes.
Gasolina: $5 cada mes
Comida: $20 cada mes.
Ahorro: $20 cada dos meses.
El mes pasado tuvo que hacer todos los pagos de la lista y este mes cumple años su mamá. ¿Cuánto es lo máximo que Francisco puede gastar en el regalo de su mamá?
A. $17.
B. $27.
C. $37.
D. $47.
En esta pregunta el estudiante tiene en cuenta que Francisco realizó todos los pagos el mes pasado y que hay pagos que debe realizar cada dos meses, por lo cual no debe pagar agua ni abonar para su ahorro programado. Por lo tanto, dispone de $30 más para comprar el regalo de cumpleaños de su mamá mientras que en los meses que hace todos los pagos le quedan 17. Respuesta: D.
Un país no cuenta con el dinero suficiente para atender algunas de sus
necesidades. Una forma en que el país podría conseguir dinero en el corto plazo
es aumentar:
A. El gasto del país en educación y salud.
B. La compra de productos en el extranjero.
C. La inversión destinada a edificios y carreteras.
D. El valor de los impuestos pagados por los ciudadanos.
En esta pregunta el estudiante debe identificar en las opciones las que corresponden a ingresos o egresos del país, y evidenciará que los impuestos representan un ingreso que permite consecución de dinero a corto plazo. Por lo tanto, su respuesta será la D.
B. La compra de productos en el extranjero.
C. La inversión destinada a edificios y carreteras.
D. El valor de los impuestos pagados por los ciudadanos.
En esta pregunta el estudiante debe identificar en las opciones las que corresponden a ingresos o egresos del país, y evidenciará que los impuestos representan un ingreso que permite consecución de dinero a corto plazo. Por lo tanto, su respuesta será la D.
La inflación es el aumento generalizado de los precios de los bienes de
la economía, es decir, si con $1000 hoy se compra un helado y en un mes $1000
pesos ya no alcanza para comprarlo es porque su precio subió, lo que significa
que hay inflación. Por lo tanto, la tasa de inflación refleja el
aumento porcentual de los precios en un cierto período.
Cada mes Juanita
hace mercado en el mismo supermercado y siempre compra la misma lista de
productos, que le cuesta $ 150.000.
Este mes la inflación aumentó un 5 %, lo que afecta a Juanita porque al
momento de pagar el mercado:
A. El costo total disminuyó 5 %.
B. El costo total aumento 10 %.
C. Juanita pagó más para poder llevar la lista de todos los meses.
D. Juanita pagó lo mismo por el mercado de todos los meses.
A. El costo total disminuyó 5 %.
B. El costo total aumento 10 %.
C. Juanita pagó más para poder llevar la lista de todos los meses.
D. Juanita pagó lo mismo por el mercado de todos los meses.
En esta pregunta el
estudiante debe identificar que una de las implicaciones que la inflación tiene
al adquirir bienes es perder poder adquisitivo. La respuesta correcta es la C.
Pedro se acaba de graduar de la universidad. Hace un mes pasó hojas de
vida para conseguir trabajo y lo contactaron de cuatro sitios para informarle
que fue seleccionado y le ofrecen estas propuestas de las cuales debe elegir:
1. Asistente, contrato por 16 meses con $1.200.000 de salario, a 10 km
de su casa y 20 % de probabilidades de ser ascendido en el primer año.
2. Asesor, contrato a 18 meses. $1.400.000, a 16 km de distancia de su casa y 40 % de ser ascendido en el primer año.
3. Analista, contrato a 17 meses, $1.500.00 de salario, a 12 km de distancia y 10 % de probabilidades de ascenso.
4. Consultor, contrato a 15 meses, $1.300.000, a 14 km y 60 % de posibilidades de ascenso.
2. Asesor, contrato a 18 meses. $1.400.000, a 16 km de distancia de su casa y 40 % de ser ascendido en el primer año.
3. Analista, contrato a 17 meses, $1.500.00 de salario, a 12 km de distancia y 10 % de probabilidades de ascenso.
4. Consultor, contrato a 15 meses, $1.300.000, a 14 km y 60 % de posibilidades de ascenso.
Pedro debe seleccionar una de las opciones de trabajo, de acuerdo con lo
más importante para él.
A. Si es su estabilidad laboral debe escoger el cargo de analista.
B. Si es su proyección profesional debe escoger el cargo de consultor.
C. Si es su nivel de ingresos debe escoger el cargo de asistente.
D. Si es su tiempo de transporte debe escoger el cargo de asesor.
El estudiante identifica que la mejor proyección profesional está asociada con la mayor probabilidad de ser ascendido en el primer año, por lo que si para Pedro lo más importante es su proyección profesional, debe escoger el cargo de Consultor.
A. Si es su estabilidad laboral debe escoger el cargo de analista.
B. Si es su proyección profesional debe escoger el cargo de consultor.
C. Si es su nivel de ingresos debe escoger el cargo de asistente.
D. Si es su tiempo de transporte debe escoger el cargo de asesor.
El estudiante identifica que la mejor proyección profesional está asociada con la mayor probabilidad de ser ascendido en el primer año, por lo que si para Pedro lo más importante es su proyección profesional, debe escoger el cargo de Consultor.
me la juego por saber:
01 11 2014
Enlaces para practicar las pruebas saber 9°
Me la juego por saber:
29 10 2014
Autoevaluación institucional:
Imprimirla desde :
página 176
25 10 14
Enlaces para el quiz de geometría sobre prismas
9.1:
9.2:
12 10 14
Quiz virtual progresiones aritméticas
9.1
06 10 14
Taller de geometría:(Realizarlo en el cuaderno antes de la evaluación virtual)
taller de
prismas, áreas y volúmenes
1.
Los lados de la base de un pilar hexagonal
regular miden 40 cm, y su altura 5 metros .Expresar en m2 el área de
la superficie.
2.
Uno de los ángulos de la base de un
paralelepípedo recto mide 70°. ¿Cuánto miden los ángulos planos de todos sus
diedros?
3.
La diagonal de una de las caras de un cubo mide
4 cm . Calcular la diagonal principal del cubo
4.
La diagonal principal de un cubo mide 6 cm. Calcular
la diagonal de las caras.
5.
Un cubo de 5 cm de arista es cortado por un
plano inclinado que contiene las diagonales de las caras opuestas. Calcular el
área de cada uno de estos cuerpos.
6.
Un cubo de 5 cm de arista es cortado por un
plano que pasa por sus 3 vértices de manera que la intersección sea un
triángulo equilátero. Calcular el área de este triángulo.
7.
Calcular el área total de un prisma de base
hexagonal de lado 5 cm y altura 15 cm.
8.
Calcular la arista de un cubo cuya área total es
de 1 dm2.
9.
Calcular la arista de un prisma triangular, si
su altura es igual al lado de la base y el área total es de 1 dm2.
10.
Una caja de leche tiene forma de prisma recto de
base cuadrada de 8 cm de lado. Su diagonal principal mide 23 cm. Calcular los
litros de leche que contiene.
11.
Calcular el volumen de un prisma de base
cuadrada de 8 cm de lado si su diagonal principal mide 23 cm
12.
Calcular el volumen de un prisma recto que tiene
por base un triángulo equilátero de 8 m de lado, y altura 14 m.
13.
Calcular el área lateral de un prisma recto que
tiene por base un triángulo equilátero de 8 m de lado, y altura 14 m.
14.
Calcular el área total de un prisma recto que
tiene por base un triángulo equilátero de 8 m de lado, y altura 14 m.
15.
Un frasco de perfume tiene forma de prisma recto
de base pentagonal regular de lado 6
cm y apotema 4 cm. Determinar cuántos ml
de perfume puede contener.
16.
Determinar el volumen de un prisma rectangular
cuya base es un hexágono de lado 2 cm y
altura 10 cm.
17.
Determinar el área lateral de un prisma
rectangular cuya base es un hexágono de
lado 2 cm y altura 10 cm.
18.
Determinar el área total de un prisma
rectangular cuya base es un hexágono de
lado 2 cm y altura 10 cm.
19.
Calcular el volumen de un prisma recto de base hexagonal si su altura es 10 cm y su
diagonal principal es la raíz cuadrada de 116 m.
20.
Calcular el área total de un prisma recto de base hexagonal si su altura es 10 cm y su
diagonal principal es la raíz cuadrada de 116 m.
05 de Octubre de 2014
Enlaces para practicar la prueba saber de 9° 2014
Me la juego por saber
Entrenamiento para preparar la próxima prueba Saber 2014
Progresiones Aritméticas. Definición y Elementos:
El prisma. Definición, partes, tipos, área, volumen y ejemplos prácticos. Cálculo de áreas y volumen de prismas
Volumen de un prisma. Ejercicio práctico.
Resumen de clase Progresiones aritméticas
Enlaces para el quiz de geometría:
9.1:
9.2:
Ecuaciones Logarítmicas Solución de una ecuación que contiene logaritmos Ecuación que contiene logaritmos Ecuación con logaritmos de bases distintas Ecuación con logaritmos de diferentes bases
Otros enlaces de interés:
Ecuaciones logarítmicas(Ejercicios)
Solución de ecuaciones logarítmicas
Actividad de apoyo para Álgebra.
Practicar ecuaciones en los siguientes enlaces, antes de presentar el quiz de apoyo.
Realizar los problemas antes de presentar el Quiz
1.Escribir una ecuación de segundo grado cuyas soluciones son: 3 y −2.
2.Factorizar:
3.Determinar k de modo que las dos raíces de la ecuación x2 − kx + 36 = 0 sean iguales.
4.La suma de dos números es 5 y su producto es −84. Halla dichos números.
5.Dentro de 11 años la edad de Pedro será la mitad del cuadrado de la edad que tenía hace 13 años. Calcula la edad de Pedro.
6.Para vallar una finca rectangular de 750 m² se han utilizado 110 m de cerca. Calcula las dimensiones de la finca.
7.Los tres lados de un triángulo rectángulo son proporcionales a los números 3, 4 y 5. Halla la longitud de cada lado sabiendo que el área del triángulo es 24 m².
8.Un jardín rectangular de 50 m de largo por 34 m de ancho está rodeado por un camino de arena uniforme. Halla la anchura de dicho camino si se sabe que su área es 540 m².
9.Calcula las dimensiones de un rectángulo cuya diagonal mide 75 m, sabiendo que es semejante a otro rectángulo cuyos lados miden 36 m y 48 m respectivamente.
10.Halla un número entero sabiendo que la suma con su inverso es 26/5
11.Dos números naturales se diferencian en dos unidades y la suma de sus cuadrados es 580. ¿Cuáles son esos números?
12.Dos caños A y B llenan juntos una piscina en dos horas, A lo hace por sí solo en tres horas menos que B. ¿Cuántas horas tarda a cada uno separadamente?
13.Los lados de un triángulo rectángulo tienen por medidas en centímetros tres números pares consecutivos. Halla los valores de dichos lados.
14.Una pieza rectangular es 4 cm más larga que ancha. Con ella se construye una caja de 840 cm3 cortando un cuadrado de 6 cm de lado en cada esquina y doblando los bordes. Halla las dimensiones de la caja.
15.Un caño tarda dos horas más que otro en llenar un depósito y abriendo los dos juntos se llena en 1 hora y 20 minutos. ¿Cuánto tiempo tardará en llenarlo cada uno por separado?
Para ambos novenos. Traer en hojas de block, resueltos los siguientes problemas:
Problemas de aplicación sector
circular corona circular trapecio circular, segmento circular.
1. Una vaca está atada a la esquina de
un granero rectangular de 4 metros de ancho por 5 metros de largo, con una
cuerda de 6 metros. Determinar el área en la que la vaca puede pastar.
2. Calcular el área del sector circular
cuya cuerda es el lado de un triángulo equilátero inscrito siendo 2 metros el
radio de la circunferencia.
3. Si el área de un sector circular de
90° es 4pi metros cuadrados. Calcular el radio del círculo al que pertenece, la
longitud del arco comprendido, el área del círculo y la longitud de la
circunferencia total.
4. Hallar el área de un sector circular
cuya cuerda es el lado de un cuadrado inscrito siendo 4 metros el radio de la
circunferencia
5. Determinar la longitud del arco de
circunferencia del Problema 4.
6. Un faro barre con su luz un ángulo
plano de 120° . Si el alcance máximo del faro es de 6 millas. Cuál es la longitud máxima en millas y en metros del
arco correspondiente.
7. Los brazos de un columpio miden 1.5
metros de largo y pueden describir como máximo un ángulo de 140°. Calcular el
espacio recorrido por el asiento del columpio cuando el ángulo descrito en su
balanceo es el máximo.
8. Calcular el área del segmento
circular del problema # 4.
Luego de resolver los problemas ya pueden realizar
el quiz virtual de apoyo en el siguiente enlace:
9.1
9.2:
Agosto 14 de 2014
Para noveno.
Presentar de álgebra los problemas de julio 26 de 2014
y de geometría los problemas de julio 15 de 2014 que aparecen es te blog,en hojas de block.
Agosto 13 de 2014
Quiz virtual de sistemas de ecuaciones lineales. Hasta 16 08 14
Para 9.2:
Para 9.1:
Problemas que se resuelven por ecuaciones de segundo grado Ej.
Aplicaciones con ecuaciones cuadráticas Ejemplo 3
Problema resuelto con ecuaciones de segundo
grado Ejemplo 4
APLICACIÓN DE ECUACIONES CUADRÁTICAS caja de latón.
Otros enlaces de interés
Ecuaciones de Segundo Grado por Fórmula General Solución de una ecuación cuadrática por fórmula general Solución de una ecuación cuadrática por factorización y fórmula. Ecuaciones de 2º grado. Fórmula General
Julio 30 de 2014
Geometría
Trapecio circular:
Julio 26 de 2014
Método de igualación
Problemas de aplicación
Julio 23 de 2014
Geometría:
Julio 20 de 2014
Geometría
Julio 17 de 2014
Otros métodos de solución de ecuaciones simultáneas.
Por determinantes ( regla de cramer)
otro video Método por igualación Otro video.
Julio 15 de 2014
Problemas de geometría.
Realizarlos en el cuaderno.
Problemas de aplicación de Geometría
sector circular
1. Una vaca está atada a la esquina de
un granero rectangular de 4 metros de ancho por 5 metros de largo, con una
cuerda de 6 metros. Determinar el área en la que la vaca puede pastar.
2. Calcular el área del sector circular
cuya cuerda es el lado de un triángulo equilátero inscrito siendo 2 metros el
radio de la circunferencia.
3. Si el área de un sector circular de
90° es 4pi metros cuadrados. Calcular el radio del círculo al que pertenece, la
longitud del arco comprendido, el área del círculo y la longitud de la
circunferencia total.
4. Hallar el área de un sector circular
cuya cuerda es el lado de un cuadrado inscrito siendo 4 metros el radio de la
circunferencia
5. Determinar la longitud del arco de
circunferencia del Problema 4.
6. Un faro barre con su luz un ángulo
plano de 120° . Si el alcance máximo del faro es de 6 millas. Cuál es la longitud máxima en millas y en metros del
arco correspondiente.
7. Los brazos de un columpio miden 1.5
metros de largo y pueden describir como máximo un ángulo de 140°. Calcular el
espacio recorrido por el asiento del columpio cuando el ángulo descrito en su
balanceo es el máximo.
Solución de un sistema de ecuaciones 2x2 por el método de reducción o eliminación:
Otra Solución por reducción: Solucion de un sistema 2x2 por método gráfico
Mayo 31 de 2014
Hacer clic en :
Para las autoevaluaciones:
Ejercicios interactivos de semejanza de
triángulos
semejanza de triang
criterios de semejanza
Viernes 4 de Abril de 2014
Enlace para descargar resumen de relaciones y funciones:
Es es para ambos novenos, para practicar y autoevaluarse:
http://www.vitutor.com/fun/1/a_2_e.html
http://www.vitutor.com/fun/1/a_3_e.html
Viernes 15 de Febrero de 2014
Taller Resumen de geometría
Descargar el ducumento de Ángulos del siguiente enlace:
26 de Febrero de 2014
Estudiar Ángulos Entre Paralelas en el enlace:
http://www.aulafacil.com/matematicas-basicas/geometria/curso/Lecc-14.htm
http://www.youtube.com/watch?v=qTQXBYkekms
27 de febrero de 2014
Taller de Potencias y Raíces.
Descargar de:
https://www.dropbox.com/s/jwsiwy9skxmk1k6/Ejercicios%20de%20N%C3%BAmeros%20Reales%20potencias%20y%20raices.doc
04 de Marzo de 2014
Notas del I Periodo 2014
Grado 9.1
Algebra:
Grado 9.1
Algebra:
geometría:
Grado 9.2
Algebra:
Geometría:
Ejercicios de Práctica de PA
1) El cuarto Término De Una Progresión aritmética de es 10, y el sexto es 16. ESCRIBIR la Progresión.2) ESCRIBIR tres Medios aritméticos Entre 3 y 23.
3) Interpolar tres Medios aritméticos Entre 8 y -12.
4) El Primer Término De Una Progresión aritmética de es -1, y el décimoquinto en 27. Hallar La Diferencia y La Suma de los Membrillos de de de de Primeros Términos.
5) Hallar la suma de los Membrillos Primeros Múltiplos de 5.
6) Números Hallar La Suma de los Membrillos acabados de Primeros ES 5.
7) Hallar La Suma de los Membrillos Primeros Números Pares Mayores de Que 5.
8) Hallar los Ángulos de cuadrilátero convexo Pecado, sabiendo Que estan en Progresión aritmética, SIENDO d = 25 º.
9) El cateto Menor entre ONU Rectángulo triángulo mide 8 cm. Aritmética Calcula Los Otros dos, sabiendo Que los Lados del triángulo Forman Una Progresión.
Taller de Apoyo definitiva:




































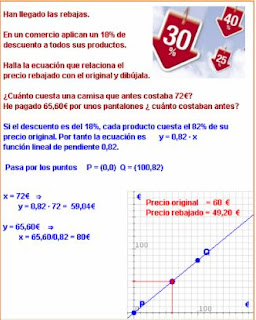









buenos días profesor Elkin, le escribe Santiago Londoño y tengo un problema para ingresar a hacer el examen virtual; la contraseña que tenia establecida no me funciona, quisiera saber que posibilidades hay de presentar elk examen otro día y que usted me reasigne otra contraseña.
ResponderEliminarA mi también que yo no me acuerdo por favor resignarme otra contraseña soy de 9-1 yo ya le habia dicho pero no le dije la contraseña nueva.
ResponderEliminarnecesito cambiar la contraseña porque se me olvido por favor profesor llamar al 595 98 84
Eliminarel teefono correcto es 5859884
ResponderEliminarProfe lo de Galileo no me entra
ResponderEliminarProfesor Elkin Buenas
ResponderEliminarMe puede hacer el gran favor de habilitarme el taller de matematicas ya que ocurrio un accidente y lo envie por equivocacion